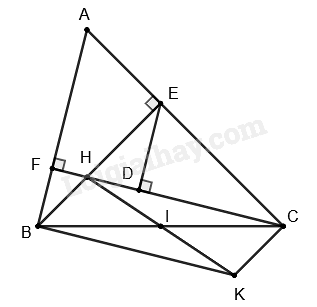
Cho tam giác ABC nhọn (AB < AC)  có hai đường cao BE, CF cắt nhau tại H

a) Chứng minh $\Delta ABE\backsim \Delta ACF$

b) Đường thẳng qua E song song với AB, cắt đoạn CH tại D. Chứng minh \(H{E^2} = HD.HC\).

c) Gọi I là trung điểm của CB. Các đường thẳng kẻ từ B song song với CF và từ C song song với BE cắt nhau tại K. Chứng minh H, I, K thẳng hàng.

a) Xét \(\Delta ABE\) và \(\Delta ACF\) có:

\(\widehat {BEA} = \widehat {CFA} = {90^0}\)

\(\widehat A\) chung

suy ra $\Delta ABE\backsim \Delta ACF$ (g.g) (đpcm)

b) Ta có DE // AB nên \(\widehat {HED} = \widehat {ABE}\) (hai góc so le trong)

\(\widehat {ACF} = \widehat {ABE}\) (do $\Delta ABE\backsim \Delta ACF$)

suy ra \(\widehat {ACF} = \widehat {HED}\)

Xét \(\Delta HED\) và \(\Delta HCE\) có:

\(\widehat H\) chung

\(\widehat {ACF} = \widehat {HED}\)

suy ra $\Delta HED\backsim \Delta HCE$ (g.g)

suy ra \(\frac{{HE}}{{HC}} = \frac{{HD}}{{HE}}\) hay \(H{E^2} = HD.HC\) (đpcm)

c) Xét tứ giác BHCK có:

BH // CK (gt)

BK // HC (gt)

suy ra BHCK là hình bình hành.

Suy ra BC và HK cắt nhau tại trung điểm của mỗi đường.

Mà I là trung điểm của BC nên I cũng là trung điểm của HK hay H, I, K thẳng hàng (đpcm).