Nội dung từ Loigiaihay.Com
Cho \(\Delta ABC\) có \(AB = 2cm,AC = 4cm\). Qua B dựng đường thẳng cắt AC tại D sao cho \(\widehat {ABD} = \widehat {ACB}\).
a) Chứng minh $\Delta ABD\backsim \Delta ACB$
b) Tính AD và DC.
c) Gọi AH là đường cao của \(\Delta ABC\), AE là đường cao của \(\Delta ABD\). Chứng minh rằng diện tích \(\Delta ABH\) gấp 4 lần diện tích \(\Delta ADE\).
a) Chứng minh $\Delta ABD\backsim \Delta ACB$ theo trường hợp góc – góc.
b) Từ $\Delta ABD\backsim \Delta ACB$ suy ra tỉ số các cặp cạnh tương ứng bằng nhau suy ra \(A{B^2} = AC.AD\), từ đó ta tính AD và DC.
c) Chứng minh $\Delta ADE\backsim \Delta ABH$ theo trường hợp góc – góc suy ra tỉ số đồng dạng giữa các cặp cạnh tương ứng để chứng minh.
Sử dụng công thức tính diện tích tam giác vuông chứng minh.
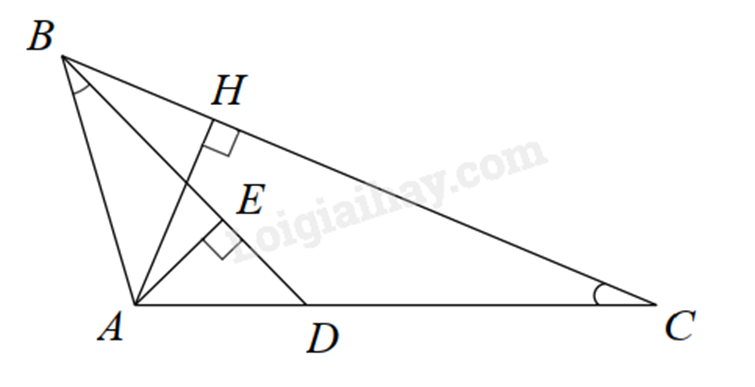
a) Xét \(\Delta ABD\) và \(\Delta ACB\) có:
\(\widehat {ABD} = \widehat {ACB}\) (gt)
\(\widehat {BAC}\) chung
Suy ra $\Delta ABD\backsim \Delta ACB$ (g.g). (đpcm)
b) Vì $\Delta ABD\backsim \Delta ACB$ (cmt) suy ra \(\frac{{AB}}{{AC}} = \frac{{AD}}{{AB}}\) nên \(A{B^2} = AC.AD\).
Suy ra \({2^2} = 4.AD\) hay \(AD = 1\left( {cm} \right)\).
Suy ra \(CD = AC - AD = 4 - 1 = 3\left( {cm} \right)\)
c) Do $\Delta ABD\backsim \Delta ACB$ suy ra \(\widehat {ADE} = \widehat {ABC}\).
Xét \(\Delta AED\) và \(\Delta AHB\) có:
\(\widehat E = \widehat H = {90^0}\)
\(\widehat {ADE} = \widehat {ABC}\)(cmt)
Suy ra $\Delta ADE\backsim \Delta ABH\left( g.g \right)$ suy ra \(\frac{{AE}}{{AH}} = \frac{{DE}}{{BH}} = \frac{{AD}}{{AB}} = \frac{1}{2}\).
Do đó \(BH = 2DE;AH = 2AE\).
Từ đó suy ra \({S_{\Delta ABH}} = \frac{1}{2}BH.AH = \frac{1}{2}\left( {2DE} \right)\left( {2AE} \right) = 4.\frac{1}{2}DE.AE = 4{S_{\Delta ADE}}\) (đpcm).

Các bài tập cùng chuyên đề
Phương trình nào sau đây là phương trình bậc nhất một ẩn?
Phương trình \(2x + 7 = 3x + 15\) có tập nghiệm là
Cho $\Delta ABC\backsim \Delta DEF$ có \(\frac{{AB}}{{DE}} = \frac{1}{2}\) và diện tích \(\Delta DEF\) bằng \(160c{m^2}\). Khi đó diện tích \(\Delta ABC\) bằng:
Cho \(\Delta MNP\) có MN = 8cm, MP = 16cm. Điểm D thuộc cạnh MN sao cho ND = 2cm, điểm E thuộc cạnh MP sao cho EP = 13cm. Khi đó \(\Delta MNP\) đồng dạng với tam giác nào?
Giải các phương trình sau:
a) \(7 - \left( {2x + 4} \right) = - \left( {x + 4} \right)\)
b) \(\frac{{1 - 3x}}{6} + x - 1 = \frac{{x + 2}}{2}\)
c) \(\frac{{8x - 3}}{4} - \frac{{3x - 2}}{2} = \frac{{2x - 1}}{2} + \frac{{x + 3}}{4}\)












