Nội dung từ Loigiaihay.Com
Giải bài toán bằng cách lập phương trình
Một xe tải và một xe con cùng khởi hành từ tỉnh A đến tỉnh B. Xe tải đi với vận tốc 30km/h, xe con đi với vận tốc 45km/h. Sau khi đi được \(\frac{3}{4}\) quãng đường AB, xe con tăng vận tốc 5km/h trên quãng đường còn lại thì đến B sớm hơn xe tải là 2 giờ 27 phút. Tính quãng đường AB.
Giải bài toán bằng cách lập phương trình.
Gọi quãng đường AB là x (km) (x > 0).
Biểu diễn thời gian xe tải, xe con đi theo x và lập phương trình.
Giải phương trình và kiểm tra nghiệm.
Gọi quãng đường AB dài x (km) (x > 0).
Thời gian xe tải đi hết quãng đường AB là \(\frac{x}{{30}}\) (giờ).
\(\frac{3}{4}\) quãng đường AB là \(\frac{3}{4}x\) (km), khi đó thời gian ô tô con đi hết \(\frac{3}{4}\) quãng đường AB là:
\(\frac{3}{4}x:45 = \frac{x}{{60}}\) (giờ)
Vận tốc xe con sau khi tăng thêm 5km/h là:
45 + 5 = 50 (km/h)
Quãng đường còn lại là: \(1 - \frac{3}{4}x = \frac{x}{4}\) (km)
Thời gian xe con đi hết \(\frac{1}{4}\) quãng đường AB là:
\(\frac{x}{4}:50 = \frac{x}{{200}}\) (h)
Vì xe con đến B sớm hơn xe tải là 2 giờ 27 phút = \(\frac{{49}}{{20}}\)h nên ta có phương trình:
\(\begin{array}{l}\frac{x}{{30}} - \left( {\frac{x}{{60}} + \frac{x}{{200}}} \right) = \frac{{49}}{{20}}\\\frac{{20x}}{{600}} - \frac{{10x}}{{600}} - \frac{{3x}}{{600}} = \frac{{1470}}{{600}}\\\frac{{7x}}{{600}} = \frac{{1470}}{{600}}\\7x = 1470\\x = 210(TM)\end{array}\)
Vậy quãng đường AB dài 210km.

Các bài tập cùng chuyên đề
Trong các phương trình sau, phương trình nào là phương trình bậc nhất một ẩn?
Với \(m = - 1\) thì phương trình \(\left( {2{m^2} - 2} \right)x = m + 1\)
Hàm số nào sau đây là hàm số bậc nhất?
Đường thẳng có hệ số góc bằng 2 và đi qua điểm (1;4) là
Giá trị m để đường thẳng \(y = \left( {m + 1} \right)x + 2\) song song với đường thẳng \(y = - 2x\) là:
Một hộp chứa 16 tấm thẻ cùng loại được đánh số từ 11 đến 26. An lấy ngẫu nhiên một thẻ từ hộp. Xác suất để thẻ chọn ra ghi số chia hết cho 4 là
Một nhà máy sản xuất laptop tiến hành kiểm tra chất lượng của 500 chiếc laptop được sản xuất và thấy có 6 chiếc bị lỗi. Trong một lô hàng có 1200 chiếc laptop. Hãy dự đoán xem có khoảng bao nhiêu chiếc laptop bị lỗi.
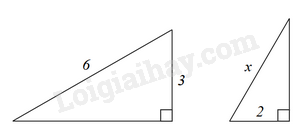
Cho hình vẽ sau. Độ lớn x bằng bao nhiêu để hai tam giác đồng dạng?
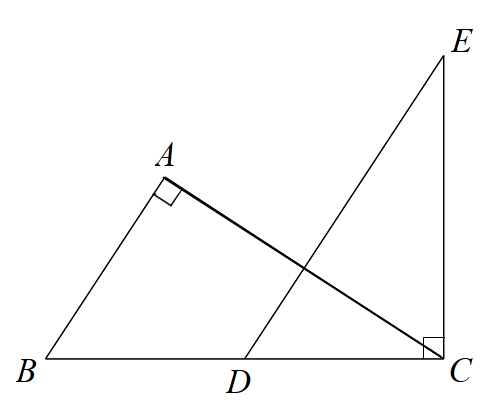
Cho hình dưới đây. Biết AB // DE. Chọn hệ thức sai trong các câu sau:
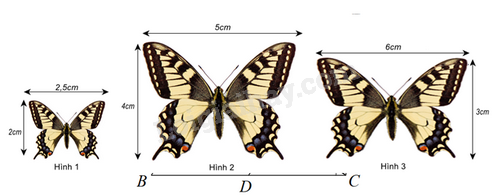
Cặp hình đồng dạng trong hình dưới đây là:
Hình chóp tam giác đều có đáy là hình gì?
Bánh ít có dạng hình chóp tứ giác đều cạnh 3cm, chiều cao 3cm. Thể tích của một chiếc bánh ít là

Cho đường thẳng \(\left( d \right):y = - 3x\) và đường thẳng \(\left( {d'} \right):y = x + 2\).
a) Vẽ đồ thị hai hàm số trên cùng một mặt phẳng tọa độ.
b) Tìm a, b để \(\left( {d''} \right):y = ax + b\) đi qua điểm \(A\left( { - 1;3} \right)\) và song song với \(\left( {d'} \right)\).
Bộ đồ chơi gồm có chim đại bàng và hình chóp để giữ thăng bằng. Biết hình chóp để giữ thăng bằng là hình chóp tứ giác đều có cạnh 40mm, chiều cao hình chóp đều đó là 52mm. Tính thể tích của hình chóp tứ giác đều đó (làm tròn kết quả đến hàng phần mười).

Cho tam giác ABC vuông tại A. Lấy điểm M sao cho AM là phân giác của góc BAC, lấy điểm N và P thuộc AC sao cho MN và MP lần lượt vuông góc với AC và BC. Chứng minh rằng:
a) $\Delta MPC\backsim \Delta ABC$.
b) \(\frac{{BC}}{{MC}} = \frac{{AB + AC}}{{AC}}\).
c) \(MP = MB\).
Nam bỏ một số viên bi xanh và đỏ có kích thước và khối lượng giống nhau vào túi. Mỗi lần Nam lấy ra ngẫu nhiên 1 viên bi, xem màu của nó rồi trả lại túi. Lặp lại phép thử đó 100 lần, Nam thấy có 40 lần mình lấy được bi đỏ. Biết rằng trong túi có 9 viên bi xanh, hãy ước lượng trong xem trong túi có bao nhiên viên bi đỏ.












