Một chất điểm chuyển động có phương trình chuyển động là  \(s = s(t) =  - {t^3} + 9{t^2} + t + 10\) (t được tính bằng giây, s được tính bẳng mét)

Tính giá trị của biểu thức \(A = \frac{{{{12}^{5 + \sqrt 3 }}}}{{{2^{5 + 2\sqrt 3 }}{{.3}^{7 + \sqrt 3 }}}}\):

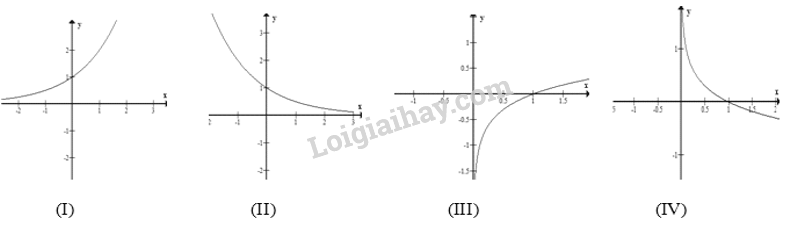
Trong các hình sau, hình nào là dạng đồ thị của hàm số \(y = {\log _a}x,0 < a < 1\)

Cho hình chóp \(SABC\) có \(SA \bot \left( {ABC} \right).\) Gọi \(H,{\rm{ }}K\) lần lượt là trực tâm các tam giác \(SBC\) và\(ABC\). Mệnh đề nào sai trong các mệnh đề sau?

Cho tứ diện \(\frac{a}{3}\) trong đó\(\left( {ACB'} \right)//(DA'C')\), \(d\left( {\left( {ACB'} \right),\left( {DA'C'} \right)} \right) = d\left( {D;\left( {ACB'} \right)} \right) = d\left( {B;\left( {ACB'} \right)} \right)\), \(BA = BB' = BC = a\) vuông góc với nhau từng đôi một và\(AB' = AC = CB' = a\sqrt 2 \), \(B.ACB'\),\(I\). Khoảng cách từ \(AC,\,\,G\) đến đường thẳng \(ACB'\) bằng

Tại một cuộc hội thảo quốc tế có 50 nhà khoa học trong đó có 31 người thành thạo tiếng Anh, 21 người thành thạo tiếng Pháp và 5 người thành thạo cả tiếng Anh và tiếng Pháp. Chọn ngẫu nhiên một người dự hội thảo. Xác suất để người được chọn thành thạo ít nhất một trong hai thứ tiếng Anh hoặc tiếng Pháp là:

Cho hàm số \(y =  - {x^3} + 3x - 2\) có đồ thị \(\left( C \right).\)Phương trình tiếp tuyến của \(\left( C \right)\) tại giao điểm của \(\left( C \right)\) với trục tung là

Cho hàm số \(y = {\sin ^2}x\). Khi đó đạo hàm y’ là

Hàm số \(y = \sqrt {2 + 2{x^2}} \)có đạo hàm \(y' = \frac{{a + bx}}{{\sqrt {2 + 2{x^2}} }}\). Khi đó \(S = a - 2b\) có kết quả bằng

Hàm số \(y = \frac{{{x^2} + x}}{{x - 1}}\)có đạo hàm \(y' = \frac{{a{x^2} + bx + c}}{{{{(x - 1)}^2}}}\). Khi đó \(S = a + b + c\) có kết quả là:

Một chất điểm chuyển động có phương trình \(s\left( t \right) = {t^2} + 1\) (\(t\) tính bằng giây, \(s\) tính bằng mét). Vận tốc tức thời của chất điểm tại thời điểm \(t = 3s\)bằng

Hai người cùng bắn vào 1 bia. Người thứ nhất có xác suất bắn trúng là 60%, xác suất bắn trúng của người thứ 2 là 70%. Xác suất để cả hai người cùng bắn trật bằng:

Hàm số \(y = {x^5}\) có đạo hàm là:

Tính giới hạn: \(I = \mathop {lim}\limits_{x \to  - 3} \frac{{{x^2} + 2x - 3}}{{{x^2} + 5x + 6}}\)

Cho hàm số : \(y = 5{x^4} - 3{x^3} + 6x - \sqrt 7 \). Tính \(f'\left( 0 \right)\).

Cho hình chóp tứ giác đều\(S.ABCD\)có tất cả các cạnh bằng \(a\). Tính khoảng cách từ đỉnh \(S\) đến mặt phẳng \((ABCD).\)

Cho hình chóp \(S.ABCD\) có đáy là hình vuông cạnh \(a\).Cạnh bên \(SA\) vuông góc với mặt phẳng \(\left( {ABCD} \right)\) và \(SA = a\sqrt 2 \).Góc giữa đường thẳng \(SC\)và mặt phẳng \(\left( {ABCD} \right)\)bằng

Cho hàm số \(f\left( x \right) = a{x^4} + b{x^2} + c\) với \(a,b,c \in \mathbb{R}\). Biết rằng đồ thị hàm số đi qua hai điểm \(A\left( {1; - 3} \right)\) và \(B\left( {2;3} \right)\), đồng thời tiếp tuyến của đồ thị tại điểm có hoành độ bằng \( - 1\) có hệ số góc bằng 2. Tính tổng \(S = a + b + c\).

Cho hàm số \(y = \frac{{x - 2}}{{x + 3}}\) có đồ thị \(\left( C \right).\) Tìm điểm \(M\) trên đồ thị \(\left( C \right)\) sao cho tiếp tuyến của \(\left( C \right)\) tại \(M\)tạo với hai trục tọa độ một tam giác có diện tích bằng \(\frac{{18}}{5}.\)