Nội dung từ Loigiaihay.Com
Đề bài
Giải các phương trình:
a) \(\frac{{2x}}{{15}} - \frac{{15 - 2x}}{{10}} = \frac{7}{6}\);
b) \(\frac{x}{{20}} - \frac{{x + 10}}{{25}} = 2\);
c) \(\frac{{2x - 37}}{3} = - 4x + 5\);
d) \(\frac{{3\left( {3x + 1} \right) + 2}}{2} - 3 = \frac{{2\left( {5x + 1} \right)}}{3} - \frac{{3x + 1}}{6}\)
Phương pháp giải
Chuyển các số hạng chứa ẩn sang một vế.
Chuyển các hằng số sang vế còn lại.
Lời giải của GV HocTot.Nam.Name.Vn
a) \(\frac{{2x}}{{15}} - \frac{{15 - 2x}}{{10}} = \frac{7}{6}\)
\(\frac{{4x}}{{30}} - \frac{{45 - 6x}}{{30}} = \frac{{35}}{{30}}\)
\(4x - 45 + 6x = 35\)
\(4x + 6x = 35 + 45\)
\(10x = 80\)
\(x = 8\)
Vậy \(x = 8\)
b) \(\frac{x}{{20}} - \frac{{x + 10}}{{25}} = 2\)
\(\frac{{5x}}{{100}} - \frac{{4x + 40}}{{100}} = \frac{{200}}{{100}}\)
\(5x - 4x - 40 = 200\)
\(x = 200 + 40\)
\(x = 240\)
Vậy \(x = 240\)
c) \(\frac{{2x - 37}}{3} = - 4x + 5\)
\(2x - 37 = 3\left( { - 4x + 5} \right)\)
\(2x - 37 = - 12x + 15\)
\(2x + 12x = 15 + 37\)
\(14x = 52\)
\(x = \frac{{26}}{7}\)
Vậy \(x = \frac{{26}}{7}\)
d) \(\frac{{3\left( {3x + 1} \right) + 2}}{2} - 3 = \frac{{2\left( {5x + 1} \right)}}{3} - \frac{{3x + 1}}{6}\)
\(\frac{{9\left( {3x + 1} \right) + 6}}{6} - \frac{{18}}{6} = \frac{{4\left( {5x + 1} \right)}}{6} - \frac{{3x + 1}}{6}\)
\(27x + 9 + 6 - 18 = 20x + 4 - 3x - 1\)
\(27x - 20x + 3x = 4 - 1 + 18 - 9\)
\(10x = 12\)
\(x = \frac{6}{5}\)
Vậy \(x = \frac{6}{5}\)
Các bài tập cùng chuyên đề
Bài 1 :
Chọn khẳng định sai.
Xem lời giải >>
Bài 2 :
Tuổi bố hiện nay gấp 2,4 lần tuổi con. 5 năm trước đây, tuổi bố gấp \(\frac{{11}}{4}\) lần tuổi con. Tính tuổi con hiện nay.
Xem lời giải >>
Bài 3 :
Với \(x = 7\) là nghiệm của phương trình nào dưới đây?
Xem lời giải >>
Bài 4 :
Hai đường thẳng \(y = - 5x\) và \(y = - 5x + 2\)
Xem lời giải >>
Bài 5 :
Cho tam giác \({\rm{ABC}}\) vuông tại \(A\) và có đường phân giác \(BD\left( {D \in AC} \right)\). Biết \(AD = 3{\rm{\;cm}},DC = 5{\rm{\;cm}}\). Tính độ dài các đoạn thẳng \({\rm{BC}}\).
Xem lời giải >>
Bài 6 :
Cho tam giác \(ABC\) vuông tại \(A\) có \(AB = 5{\rm{\;cm}}\) và \(BC = 13{\rm{\;cm}}\). Qua trung điểm \(M\) của \({\rm{AB}}\), vẽ một đường thẳng song song với \({\rm{AC}}\) cắt \({\rm{BC}}\) tại \({\rm{N}}\). Tính độ dài \({\rm{MN}}\).
Xem lời giải >>
Bài 7 :
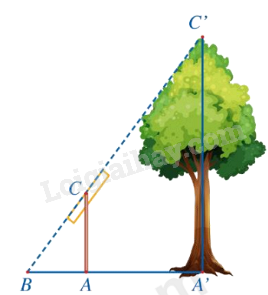
Trong hình dưới đây, độ dài đoạn thẳng \({\rm{A'C'}}\) mô tả chiều cao của một cái cây, đoạn thẳng \({\rm{AC}}\) mô tả chiều cao của một cái cọc (cây và cọc cùng vuông góc với đường thẳng đi qua ba điểm \(\left. {A',A,B} \right)\). Giả sử \(AC = 2{\rm{\;m}},AB = 1,5{\rm{\;m}},A'B = 4,5{\rm{\;m}}\). Tính chiều cao của cây.
Xem lời giải >>
Bài 8 :
Tìm hệ số góc của mỗi đường thẳng sau:
a) \(y = - 1,7x - 1,7\);
b) \(y = - \sqrt 5 x + 1\);
c) \(y = \frac{9}{{ - 11}}x + \frac{{15}}{8}\)
d) \(y = \frac{1}{{\sqrt 3 }}x - \sqrt {11} \).
Xem lời giải >>
Bài 9 :
Giá niêm yết của một máy lọc nước và một nồi cơm điện có tổng là 6,5 triệu đồng. Bác Bình mua hàng vào đúng dịp tri ân khách hàng nên so với giá niêm yết máy lọc nước được giảm giá \(15{\rm{\% }}\) và nồi cơm điện được giảm giá \(10{\rm{\% }}\). Do đó, tổng số tiền bác phải trả là 5,65 triệu đồng. Tính giá tiền niêm yết của mỗi sản phẩm đã nêu.
Xem lời giải >>
Bài 10 :
Hiện tại, cô Hạnh đã tiết kiệm được 500 triệu đồng. Để thực hiện dự định mua một căn chung cư có giá trị 2,6 tỉ đồng, cô Hạnh đã lên kế hoạch hằng tháng tiết kiệm 15 triệu đồng. Gọi y (triệu đồng) là số tiền cô Hạnh tiết kiệm được sau \(x\) (tháng) kể từ hiện tại.
a) Viết công thức tính \(y\) theo \(x\). Hỏi \(y\) có phải là hàm số bậc nhất của \(x\) hay không?
b) Hỏi sau bao lâu kể từ hiện tại thì cô Hạnh có thể mua được căn hộ chung cư đó bằng tiền tiết kiệm?
Xem lời giải >>