Hai tổ sản xuất cùng may một loại áo. Nếu tổ thứ nhất may trong 5 ngày, tổ thứ hai may trong 7 ngày thì cả hai tổ may được 1000 chiếc áo. Biết rằng năng suất lao động của tổ thứ nhất hơn tổ thứ hai là 8 chiếc áo/ngày. Tính năng suất lao động của mối tỗ.

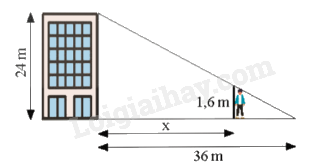
Một toà nhà cao \(24{\rm{\;m}}\), đổ bóng nắng dài \(36{\rm{\;m}}\) trên đường như hình sau. Một người cao 1,6 m muốn đứng trong bóng râm của toà nhà. Hỏi người đó có thể đứng cách toà nhà xa nhất bao nhiêu mét?

Bạn Băng tung đồng xu 10 lần liên tiếp và được kết quả như bảng sau, biết mặt ngửa (N) và mặt sấp \(\left( {\rm{S}} \right)\).

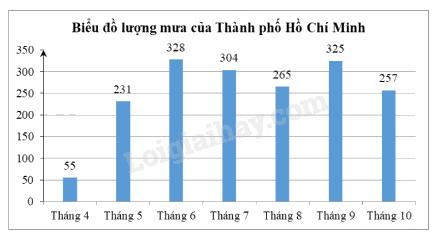
Cho biểu đồ lượng mưa (đơn vị: \({\rm{mm}}\) ) ở Thành phố Hồ Chí Minh từ tháng 4 đến tháng 10 trong một năm như hình bên. Trong các phát biểu sau, chọn phát biểu đúng.

Tìm \(x\) trong hình dưới đây:

Giải phương trình \(\frac{1}{2}\left( {x + 5} \right) - 4 = \frac{1}{3}\left( {2x - 1} \right)\) ta được:

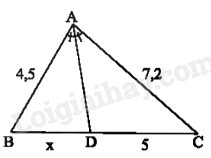
Cho \(\Delta ABC\) có \(AB = 6{\rm{\;cm}},AC = 8{\rm{\;cm}},BC = 10{\rm{\;cm}}\). Gọi \({\rm{H}},I,{\rm{\;K}}\) lần lượt là trung điểm của \({\rm{AB}},{\rm{BC}},{\rm{AC}}\). Chu vi tứ giác \({\rm{AHIK}}\) bằng:

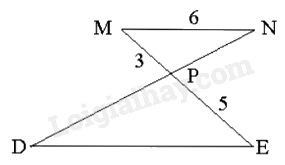
Cho hình vẽ, biết \({\rm{MN}}//{\rm{DE}},{\rm{MN}} = 6{\rm{\;cm}},{\rm{MP}} = 3{\rm{\;cm}},{\rm{PE}} = 5{\rm{\;cm}}\). Độ dài đoạn thẳng \({\rm{DE}}\) là:

Phương trình nào sau đây là phương trình bậc nhất một ẩn?

Người ta đặt các trạm đo mưa tự động trên toàn quốc để phục vụ cho công tác phòng, chống thiên tai của các tỉnh, thành phố, các hồ thủy lợi, thuỷ điện trên toàn quốc. Dữ liệu gừi về từ các trạm được hiển thị trên một website với các thông tin: Địa điểm, Lượng mưa (đo bằng mm) và Mức độ mưa (Không mưa, mưa nhỏ, mưa vừa, mưa to).

Người ta đã thực hiện thu thập dữ liệu bằng cách:

Một công ty nước giải khát quảng cáo soda cam của họ là "có hương vị tự nhiên", mặc dù nó chỉ chứa \(5{\rm{\% }}\) nước cam. Theo quy định, một nước uống được gọi là "có hương vị tự nhiên" phải chứa ít nhất \(10{\rm{\% }}\) nước trái cây. Nhà sản xuất này phải thêm ít nhất bao nhiêu mililít nước cam nguyên chất vào 900ml soda cam để đảm bảo yêu cầu này?

Giải các phương trình sau:
a) \(4x - 2 = x + 5\);
b) \( - 2x - 5 = 5x - 7\);
c) \(2\left( {2x - 1} \right) = 5\left( {x - 1} \right)\).

Một tấm bìa cứng hình tròn được chia thành 20 hình quạt như nhau, đánh số 1;2;..;20 và được gắn vào trục quay có mũi tên cố định ở tâm. Quay tấm bìa và quan sát xem mũi tên chỉ vào hình quạt nào khi tấm bìa dừng lại.

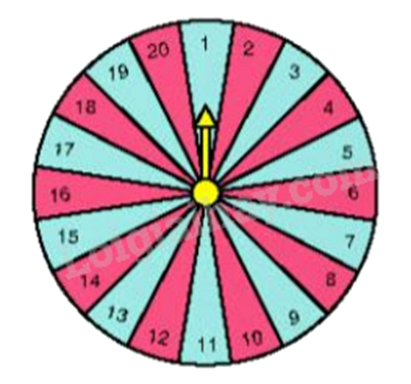
Tính xác suất để mũi tên:

a) Chỉ vào hình quạt ghi số chia hết cho 4 .

b) Chỉ vào hình quạt ghi số không phải là số nguyên tố.

Một hộp chứa 3 viên bi xanh, 4 viên bi đỏ và 5 viên bi vàng có kích thước và khối lượng giống nhau. Lấy ra ngẫu nhiên 1 viên bi từ hộp. Tính xác suất của các biến cố:

a) A: "Viên bi lấy ra có màu xanh";

b) B: "Viên bi lấy ra không có màu đỏ".

Cho tam giác \({\rm{ABC}}\) vuông tại \(A(AB < AC)\), kẻ đường cao \({\rm{AH}}\), đường trung tuyến \({\rm{AM}}\). Đường thẳng vuông góc với \({\rm{AM}}\) tại \(A\) cắt đường thẳng \({\rm{BC}}\) tại \(D\). Chứng minh rằng:
a) \({\rm{AB}}\) là tia phân giác của \(\widehat {DAH}\).
b) \(BH.CD = BD.CH\).