Nội dung từ Loigiaihay.Com
Cho hàm số: y=log[(m−2)x2+2(m+1)x+2m].
a) Với m=3, hãy tìm tập xác định của hàm số trên.
b) Tìm tất cả các giá trị của tham số m để hàm số trên có tập xác định với mọi giá trị thực của x.
Hàm số y=logu(x) xác định khi u(x)>0.
a) Với m=3 ta có: y=log(x2+8x+6).
Hàm số y=log(x2+8x+6) xác định khi x2+8x+6>0⇔[x>−4+√10x<−4−√10
Vậy với m=3 thì tập xác định của hàm số là: D=(−∞;−4−√10)∪(−4+√10;+∞).
b) Hàm số y=log[(m−2)x2+2(m+1)x+2m] xác định với mọi giá trị thực của x khi và chỉ khi f(x)=(m−2)x2+2(m+1)x+2m>0 với mọi x∈R
Trường hợp 1: Với m=2 ta có: f(x)=6x+4>0⇔x>−23.
Do đó, f(x) không xác định với mọi giá trị thực của x. Do đó, m=2 không thỏa mãn.
Trường hợp 2: Với m≠2.
Hàm số f(x)=(m−2)x2+2(m+1)x+2m>0 với mọi x∈R
⇔{m−2>0Δ′=(m+1)2−(m−2)2m<0⇔{m>2−m2+6m+1<0⇔{m>2[m<3−√10m>3+√10⇔m>3+√10
Vậy với m∈(3+√10;+∞) thì hàm số y=log[(m−2)x2+2(m+1)x+2m] có tập xác định với mọi giá trị thực của x.

Các bài tập cùng chuyên đề
Khẳng định nào sau đây là đúng?
Chọn đáp án đúng.
Cho số thực a và số nguyên dương n (n≥2). Số b được gọi là căn bậc n của số a nếu:
Chọn đáp án đúng:
Rút gọn biểu thức (93+√3−9√3−1).3−2√3 được kết quả là:
Cho a, b là các số thực dương. Rút gọn biểu thức (4√a3b2)83√√a12b6
Chọn đáp án đúng.
Chọn đáp án đúng.
Cho a, b là các số thực dương. Giá trị của lnab+lnba bằng:
Chọn đáp án đúng.
Cho a>0,a≠1,b>0. Với mọi số nguyên dương n≥2 ta có:
Cho logab=4. Giá trị của loga(a3b2) bằng:
Cho hai số thực dương a, b thỏa mãn a3b2=1000. Giá trị của biểu thức P=3loga+2logb là:
Trong các hàm số dưới đây, hàm số nào nghịch biến trên (0;+∞)?
Hàm số nào dưới đây là hàm số đồng biến trên R?
Đồ thị hàm số y=62x luôn đi qua điểm nào dưới đây?
Chọn đáp án đúng.
Hàm số y=logx có cơ số là:
Cho ba số thực dương a, b, c khác 1. Đồ thị các hàm số y=logax,y=logbx,y=logcx thể hiện ở hình vẽ dưới đây.
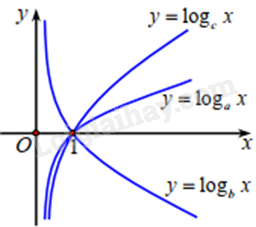
Khẳng định nào dưới đây là đúng?
Tập xác định của hàm số y=1√3−x+ln(x−1) là:
Bất phương trình 6x≥b có tập nghiệm là R khi:
Tập nghiệm của bất phương trình (1π)x>(1π)3 là:
Tập nghiệm của bất phương trình logx≥2 là:
Cho phương trình 4x+2x+2−5=0. Đặt t=2x ta được phương trình là:












