Nội dung từ Loigiaihay.Com
Cho hình chóp S. ABCD có ABCD là hình vuông cạnh bằng a và các cạnh bên đều bằng a. Gọi M, N lần lượt là trung điểm của AD, SD. Góc giữa hai đường thẳng MN và SC bằng:
-
A.
\({90^0}\).
-
B.
\({60^0}\).
-
C.
\({30^0}\).
-
D.
\({70^0}\).
Góc giữa hai đường thẳng a và b trong không gian là góc giữa hai đường thẳng a’ và b’ cùng đi qua một điểm O và lần lượt song song (hoặc trùng) với a và b; kí hiệu \(\left( {a,b} \right)\) hoặc \(\widehat {\left( {a;b} \right)}\).
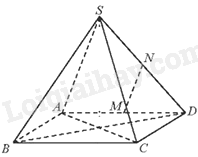
Vì M, N lần lượt là trung điểm của AD, SD nên MN là đường trung bình của tam giác SAD. Do đó, MN//AS. Suy ra, \(\left( {MN,SC} \right) = \left( {SA,SC} \right) = \widehat {SAC}\).
Vì tam giác ABC vuông tại B nên \(A{C^2} = A{B^2} + B{C^2} = 2{a^2}\)
Vì \(A{C^2} = S{A^2} + A{C^2}\) nên tam giác SAC vuông tại S (định lí Pythagore đảo)
Do đó, \(\widehat {ASC} = {90^0}\). Vậy \(\left( {MN,SC} \right) = {90^0}\).
Đáp án A.
Đáp án : A

Các bài tập cùng chuyên đề
Khẳng định nào sau đây là đúng?
Chọn đáp án đúng.
Cho số thực a và số nguyên dương n \(\left( {n \ge 2} \right)\). Số b được gọi là căn bậc n của số a nếu:
Chọn đáp án đúng:
Rút gọn biểu thức \(\left( {{9^{3 + \sqrt 3 }} - {9^{\sqrt 3 - 1}}} \right){.3^{ - 2\sqrt 3 }}\) được kết quả là:
Cho a, b là các số thực dương. Rút gọn biểu thức \(\frac{{{{\left( {\sqrt[4]{{{a^3}{b^2}}}} \right)}^8}}}{{\sqrt[3]{{\sqrt {{a^{12}}{b^6}} }}}}\)
Chọn đáp án đúng.
Chọn đáp án đúng.
Cho a, b là các số thực dương. Giá trị của \(\ln \frac{a}{b} + \ln \frac{b}{a}\) bằng:
Chọn đáp án đúng.
Cho \(a > 0,a \ne 1,b > 0\). Với mọi số nguyên dương \(n \ge 2\) ta có:
Cho \({\log _a}b = 4\). Giá trị của \({\log _a}\left( {{a^3}{b^2}} \right)\) bằng:
Cho hai số thực dương a, b thỏa mãn \({a^3}{b^2} = 1000\). Giá trị của biểu thức \(P = 3\log a + 2\log b\) là:
Trong các hàm số dưới đây, hàm số nào nghịch biến trên \(\left( {0; + \infty } \right)\)?
Hàm số nào dưới đây là hàm số đồng biến trên \(\mathbb{R}\)?
Đồ thị hàm số \(y = {6^{2x}}\) luôn đi qua điểm nào dưới đây?
Chọn đáp án đúng.
Hàm số \(y = \log x\) có cơ số là:
Cho ba số thực dương a, b, c khác 1. Đồ thị các hàm số \(y = {\log _a}x,y = {\log _b}x,y = {\log _c}x\) thể hiện ở hình vẽ dưới đây.
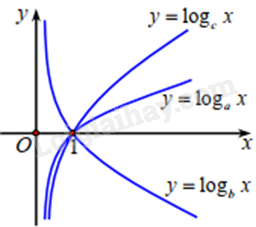
Khẳng định nào dưới đây là đúng?
Tập xác định của hàm số \(y = \frac{1}{{\sqrt {3 - x} }} + \ln \left( {x - 1} \right)\) là:
Bất phương trình \({6^x} \ge b\) có tập nghiệm là \(\mathbb{R}\) khi:
Tập nghiệm của bất phương trình \({\left( {\frac{1}{\pi }} \right)^x} > {\left( {\frac{1}{\pi }} \right)^3}\) là:
Tập nghiệm của bất phương trình \(\log x \ge 2\) là:
Cho phương trình \({4^x} + {2^{x + 2}} - 5 = 0\). Đặt \(t = {2^x}\) ta được phương trình là:












