Nội dung từ Loigiaihay.Com
Công thức \(M = {M_o}{\left( {\frac{1}{2}} \right)^{\frac{t}{T}}}\) cho biết khối lượng của một chất phóng xạ sau thời gian t kể từ thời điểm nào đó (gọi là thời điểm ban đầu), \({M_o}\) là khối lượng ban đầu, T là chu kì bán rã của chất phóng xạ đó (cứ sau mỗi chu kì, khối lượng của chất phóng xạ giảm đi một nửa). Trong một phòng thí nghiệm, với khối lượng 200g radon ban đầu, sau 16 ngày chỉ còn 11g. Chu kì bán rã của radon bằng (làm tròn kết quả đến hàng phần mười):
-
A.
3,8 ngày.
-
B.
4 ngày.
-
C.
3,5 ngày.
-
D.
4,2 ngày.
Phương trình \({a^x} = b\left( {a > 0,a \ne 1} \right)\) với \(b > 0\) có nghiệm là \(x = {\log _a}b\)
Với \({M_o} = 200g,t = 16,M = 11g\) thay vào công thức \(M = {M_o}{\left( {\frac{1}{2}} \right)^{\frac{t}{T}}}\) ta có:
\(11 = 200{\left( {\frac{1}{2}} \right)^{\frac{{16}}{T}}} \Leftrightarrow \frac{{16}}{T} = {\log _{\frac{1}{2}}}\frac{{11}}{{200}} = {\log _2}\frac{{200}}{{11}} \Leftrightarrow T = \frac{{16}}{{{{\log }_2}\frac{{200}}{{11}}}} \approx 3,8\) (ngày)
Đáp án A.
Đáp án : A

Các bài tập cùng chuyên đề
Khẳng định nào sau đây là đúng?
Chọn đáp án đúng.
Cho số thực a và số nguyên dương n \(\left( {n \ge 2} \right)\). Số b được gọi là căn bậc n của số a nếu:
Chọn đáp án đúng:
Rút gọn biểu thức \(\left( {{9^{3 + \sqrt 3 }} - {9^{\sqrt 3 - 1}}} \right){.3^{ - 2\sqrt 3 }}\) được kết quả là:
Cho a, b là các số thực dương. Rút gọn biểu thức \(\frac{{{{\left( {\sqrt[4]{{{a^3}{b^2}}}} \right)}^8}}}{{\sqrt[3]{{\sqrt {{a^{12}}{b^6}} }}}}\)
Chọn đáp án đúng.
Chọn đáp án đúng.
Cho a, b là các số thực dương. Giá trị của \(\ln \frac{a}{b} + \ln \frac{b}{a}\) bằng:
Chọn đáp án đúng.
Cho \(a > 0,a \ne 1,b > 0\). Với mọi số nguyên dương \(n \ge 2\) ta có:
Cho \({\log _a}b = 4\). Giá trị của \({\log _a}\left( {{a^3}{b^2}} \right)\) bằng:
Cho hai số thực dương a, b thỏa mãn \({a^3}{b^2} = 1000\). Giá trị của biểu thức \(P = 3\log a + 2\log b\) là:
Trong các hàm số dưới đây, hàm số nào nghịch biến trên \(\left( {0; + \infty } \right)\)?
Hàm số nào dưới đây là hàm số đồng biến trên \(\mathbb{R}\)?
Đồ thị hàm số \(y = {6^{2x}}\) luôn đi qua điểm nào dưới đây?
Chọn đáp án đúng.
Hàm số \(y = \log x\) có cơ số là:
Cho ba số thực dương a, b, c khác 1. Đồ thị các hàm số \(y = {\log _a}x,y = {\log _b}x,y = {\log _c}x\) thể hiện ở hình vẽ dưới đây.
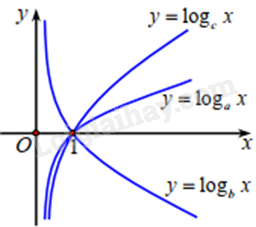
Khẳng định nào dưới đây là đúng?
Tập xác định của hàm số \(y = \frac{1}{{\sqrt {3 - x} }} + \ln \left( {x - 1} \right)\) là:
Bất phương trình \({6^x} \ge b\) có tập nghiệm là \(\mathbb{R}\) khi:
Tập nghiệm của bất phương trình \({\left( {\frac{1}{\pi }} \right)^x} > {\left( {\frac{1}{\pi }} \right)^3}\) là:
Tập nghiệm của bất phương trình \(\log x \ge 2\) là:
Cho phương trình \({4^x} + {2^{x + 2}} - 5 = 0\). Đặt \(t = {2^x}\) ta được phương trình là:












