Nội dung từ Loigiaihay.Com
Ba người cùng đi săn A, B, C độc lập với nhau cùng nổ súng bắn vào mục tiêu. Biết rằng xác suất bắn trúng mục tiêu của A, B, C lần lượt là 0,5; 0,6; 0,7. Xác suất để có ít nhất một người xạ thủ bắn trúng là:
-
A.
0,45.
-
B.
0,8.
-
C.
0,75.
-
D.
0,94.
Nếu hai biến cố A và B độc lập thì \(P\left( {A \cap B} \right) = P\left( A \right).P\left( B \right)\).
Xác suất để người A bắn trượt là: \(1 - 0,5 = 0,5\)
Xác suất để người B bắn trượt là: \(1 - 0,6 = 0,4\)
Xác suất để người C bắn trượt là: \(1 - 0,7 = 0,3\)
Xác suất để cả ba người đều bắn trượt là: \(0,3.0,4.0,5 = 0,06\)
Vậy xác suất để có ít nhất một người xạ thủ bắn trúng là: \(1 - 0,06 = 0,94\)
Đáp án D.
Đáp án : D

Các bài tập cùng chuyên đề
Mỗi nhóm số liệu gồm một số giá trị của mẫu số liệu được ghép nhóm theo một tiêu chí xác định có dạng \(\left[ {a;b} \right)\). Giá trị đại diện của nhóm \(\left[ {a;b} \right)\) là:
Nếu hai biến cố A và B độc lập thì:
Bảng tần số ghép nhóm dưới đây thể hiện thời gian sử dụng Internet trong một ngày của 40 học sinh (đơn vị: phút):
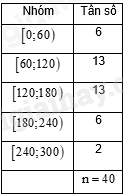
Có bao nhiêu học sinh có thời gian sử dụng Internet ít hơn 120 phút một ngày?
Cho A, B là hai biến cố của cùng một phép thử có không gian mẫu \(\Omega \). Phát biểu nào dưới đây là sai?
Cho A và B là hai biến cố độc lập với nhau. Biết rằng \(P\left( A \right) = 0,4\) và \(P\left( {\overline A B} \right) = 0,3\). Xác suất của biến cố \(A \cup B\) là:
Bảng tần số ghép nhóm số liệu dưới đây thống kê cân nặng của 40 học sinh lớp 11A trong một trường trung học phổ thông (đơn vị: kilôgam):
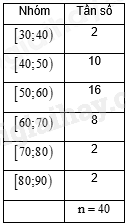
Tứ phân vị thứ ba của mẫu số liệu ghép nhóm đó là:
Tính giá trị biểu thức \(P = {\left( {\sqrt[3]{{9 + \sqrt {80} }}} \right)^{2023}}.{\left( {3 - \sqrt[3]{{9 + \sqrt {80} }}} \right)^{2024}}\)












