Nội dung từ Loigiaihay.Com
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, tam giác SAB đều và \(SC = a\sqrt 2 \). Gọi H là trung điểm của AB. Hình chiếu vuông góc của điểm S trên mặt phẳng (ABCD) là điểm:
-
A.
A.
-
B.
B.
-
C.
C.
-
D.
H.
+ Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau a và b cùng nằm trong mặt phẳng (P) thì \(d \bot \left( P \right)\).
+ Cho mặt phẳng (P). Xét một điểm M tùy ý trong không gian. Gọi d là đường thẳng đi qua điểm M và vuông góc với (P). Gọi M’ là giao điểm của đường thẳng d và mặt phẳng (P). Khi đó, điểm M’ được gọi là hình chiếu vuông góc của điểm M lên mặt phẳng (P).
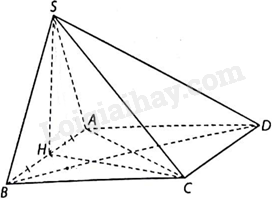
Vì tam giác ABS đều nên SH là đường trung tuyến đồng thời là đường cao.
Áp dụng định lí Pythagore vào tam giác SHB vuông tại H có:
\(SH = \sqrt {S{B^2} - H{B^2}} = \sqrt {{a^2} - {{\left( {\frac{a}{2}} \right)}^2}} = \frac{{a\sqrt 3 }}{2}\)
Áp dụng định lí Pythagore vào tam giác CHB vuông tại B có:
\(CH = \sqrt {B{C^2} + H{B^2}} = \sqrt {{a^2} + {{\left( {\frac{a}{2}} \right)}^2}} = \frac{{a\sqrt 5 }}{2}\)
Ta có: \(S{H^2} + H{C^2} = S{C^2}\left( {do\;{{\left( {\frac{{a\sqrt 3 }}{2}} \right)}^2} + {{\left( {\frac{{a\sqrt 5 }}{2}} \right)}^2} = {{\left( {a\sqrt 2 } \right)}^2}} \right)\) nên tam giác SHC vuông tại H.
Suy ra: \(SH \bot HC\)
Lại có: \(SH \bot AB\), HC và AB cắt nhau tại H và nằm trong mặt phẳng (ABCD).
Do đó, \(SH \bot \left( {ABCD} \right)\). Vậy H là hình chiếu vuông góc của S trên mặt phẳng (ABCD).
Đáp án D.
Đáp án : D

Các bài tập cùng chuyên đề
Cho \(a > 0,m,n \in \mathbb{R}\). Khẳng định nào sau đây là đúng?
Chọn đáp án đúng.
Cho số dương a. Khi đó:
Chọn đáp án đúng:
Rút gọn biểu thức \(\frac{{{x^{\frac{4}{3}}}y + x{y^{\frac{4}{3}}}}}{{\sqrt[3]{x} + \sqrt[3]{y}}}\) (với \(x,y > 0\)) được kết quả là:
Giả sử cường độ ánh sáng I dưới mặt biển giảm dần theo độ sâu theo công thức \(I = {I_o}{a^d}\), trong đó \({I_o}\) là cường độ ánh sáng tại mặt nước biển, a là một hằng số dương, d là độ sâu tính từ mặt nước biển (tính bằng mét). Ở một vùng biển cường độ ánh sáng tại độ sâu 1m bằng 90% cường độ ánh sáng tại mặt nước biển. Giá trị của a là:
Chọn đáp án đúng.
Với \(a,b > 0\) thì:
Chọn đáp án đúng.
Với \(0 < a \ne 1\) thì:
Trong Hóa học, độ pH của một dung dịch được tính theo công thức \(pH = - \log \left[ {{H^ + }} \right]\), trong đó \(\left[ {{H^ + }} \right]\) là nồng độ ion hydrogen tính bằng mol/lít. Tính nồng độ pH của dung dịch có nồng độ ion hydrogen bằng 0,001 mol/lít.
Chọn đáp án đúng: (Các biểu thức trên đều có nghĩa)
Đồ thị hàm số \(y = {\log _a}x\left( {a > 0,a \ne 1} \right)\) luôn:
Hàm số nào dưới đây là hàm số mũ cơ số 3?
Hàm số nào dưới đây không phải là hàm số lôgarit?
Hàm số \(y = {\log _a}x\left( {a > 0,a \ne 1} \right)\) liên tục trên:
Cho đồ thị các hàm số \(y = {a^x},y = {b^x},y = {\log _c}x\) như hình vẽ dưới
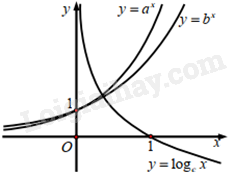
Khẳng định nào dưới đây là đúng?
Cho hàm số \(y = f\left( x \right) = {\log _{\sqrt 3 }}x\). Biết rằng: \(\mathop {\max }\limits_{x \in \left[ {3;9} \right]} y = M,\mathop {\min }\limits_{x \in \left[ {3;9} \right]} y = m\). Khi đó:
Bất phương trình \({a^x} > b\left( {0 < a \ne 1} \right)\) có tập nghiệm là \(\mathbb{R}\) khi:
Tập nghiệm của bất phương trình \({\left( {\sqrt 5 } \right)^x} > 5\) là:
Phương trình \({\log _{\frac{1}{2}}}x = - 2\) có nghiệm là:
Nếu x và y thỏa mãn \({4^x} = 16\) và \({3^{x + y}} = 729\) thì y bằng:












