Nội dung từ Loigiaihay.Com
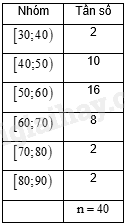
Bảng tần số ghép nhóm số liệu dưới đây thống kê cân nặng của 40 học sinh lớp 11A trong một trường trung học phổ thông (đơn vị: kilôgam). Cân nặng trung bình của 40 học sinh đó là:
-
A.
54kg.
-
B.
51kg.
-
C.
55kg.
-
D.
56kg.
Bảng tần số ghép nhóm cho ở bảng dưới:
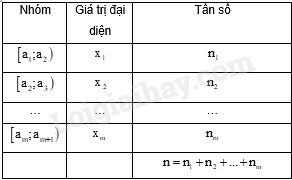
+ Trung điểm \({x_i}\) của nửa khoảng (tính bằng trung bình cộng hai đầu mút) ứng với nhóm i là giá trị đại diện của nhóm đó.
+ Số trung bình cộng của mẫu số liệu ghép nhóm, kí hiệu \(\overline x \), được tính theo công thức: \(\overline x = \frac{{{n_1}{x_1} + {n_2}{x_2} + ... + {n_m}{x_m}}}{n}\)
Ta có bảng:

Vậy cân nặng trung bình của 40 học sinh là:\(\overline x = \frac{{35.2 + 45.10 + 55.16 + 65.8 + 75.2 + 85.2}}{{40}} = 56\left( {kg} \right)\)
Đáp án D.
Đáp án : D

Các bài tập cùng chuyên đề
Mỗi nhóm số liệu gồm một số giá trị của mẫu số liệu được ghép nhóm theo một tiêu chí xác định có dạng \(\left[ {a;b} \right)\). Độ dài của nhóm \(\left[ {a;b} \right)\) là:
Cho hai biến cố A và B. Chọn đáp án đúng.
Kết quả kiểm tra môn Tiếng Anh của lớp 11E được cho ở bảng tần số ghép nhóm sau:

Nhóm \(\left[ {7;9} \right)\) có tần số là:
Cho hai biến cố A và B, biến cố giao của hai biến cố A và B kí hiệu là:
Một hộp có 12 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1; 2; 3; …; 12; hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên một chiếc thẻ trong hộp. Gọi A là biến cố: “Số xuất hiện trên thẻ rút ra là số chia hết cho 3”, B là biến cố: “Số xuất hiện trên thẻ rút ra là số chia hết cho 2”. Chọn đáp án đúng.
Cho hai biến cố độc lập A và B. Biết rằng \(P\left( A \right) = 0,4\) và \(P\left( B \right) = 0,6\). Xác suất của biến cố \(\overline A B\) là:
Cho \(a{x^3} = b{y^3} = c{z^3}\) và \(\frac{1}{x} + \frac{1}{y} + \frac{1}{z} = 1\) (với x, y, z khác 0). Chứng minh rằng:
\(\sqrt[3]{a} + \sqrt[3]{b} + \sqrt[3]{c} = \sqrt[3]{{a{x^2} + b{y^2} + c{z^2}}}\).












