Nội dung từ Loigiaihay.Com
Cho hình chóp S.ABC có \(SA \bot \left( {ABC} \right)\) và tam giác ABC vuông tại B. Kẻ \(AH \bot SB\left( {H \in SB} \right)\). Khẳng định nào dưới đây là sai?
-
A.
\(BC \bot SA\).
-
B.
\(BC \bot AH\).
-
C.
\(AH \bot AC\).
-
D.
\(AH \bot SC\).
+ Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau a và b cùng nằm trong mặt phẳng (P) thì \(d \bot \left( P \right)\).
+ Nếu một đường thẳng vuông góc với một mặt phẳng thì nó vuông góc với mọi đường thẳng nằm trong mặt phẳng đó.
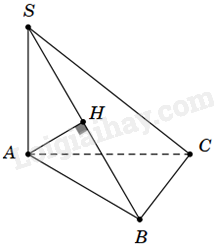
Vì \(SA \bot \left( {ABC} \right),BC \subset \left( {ABC} \right) \Rightarrow SA \bot BC\).
Tam giác ABC vuông tại B nên \(AB \bot BC\)
Ta có: \(SA \bot BC\), \(AB \bot BC\), SA và AB cắt nhau tại A và nằm trong mặt phẳng (SAB) nên \(BC \bot \left( {SAB} \right)\). Mà \(AH \subset \left( {SAB} \right) \Rightarrow BC \bot AH\)
Ta có: \(BC \bot AH,AH \bot SB\), SB và BC cắt nhau tại B và nằm trong mặt phẳng (SBC). Do đó, \(AH \bot \left( {SBC} \right)\), mà \(SC \subset \left( {SBC} \right) \Rightarrow SC \bot AH\)
Nếu \(AH \bot AC\), mà \(SA \bot AC \Rightarrow AC \bot \left( {SAH} \right) \Rightarrow AB \bot AC\) (vô lí)
Đáp án C.
Đáp án : C

Các bài tập cùng chuyên đề
Cho số thực dương a và số hữu tỉ \(r = \frac{m}{n}\), trong đó \(m,n \in \mathbb{Z},n > 0\). Ta có:
Chọn đáp án đúng
Cho a, b là những số thực dương, \(\alpha \) là số thực bất kì. Khi đó:
Chọn đáp án đúng:
Rút gọn biểu thức \({\left( {{a^{\sqrt 3 }}.{b^{\frac{{ - 6}}{{\sqrt 3 }}}}} \right)^{\frac{1}{{\sqrt 3 }}}}\) (với \(a,b > 0\)) được kết quả là:
Giá trị của biểu thức \({\left( {\sqrt 5 - 2} \right)^{2024}}.{\left( {\sqrt 5 + 2} \right)^{2025}}\)
Chọn đáp án đúng.
Với \(0 < a \ne 1,b,c > 0\) thì:
Chọn đáp án đúng.
Với a, b, c là các số dương và \(a \ne 1,b \ne 1\) thì:
Khẳng định nào sau đây đúng?
Tính \({\log _8}1250\) theo a biết \(a = {\log _2}5\).
Chọn đáp án đúng:
Đồ thị hàm số \(y = {\log _a}x\left( {a > 0,a \ne 1} \right)\) đi qua điểm:
Hàm số nào dưới đây là hàm số lôgarit cơ số 2?
Hàm số nào dưới đây nghịch biến trên \(\mathbb{R}\)?
Tập giá trị của hàm số \(y = {a^x}\left( {a > 0,a \ne 1} \right)\) là:
Tập xác định của hàm số \(y = {8^{\sqrt {{x^2} - 4} }}\) là:
Cho hàm số \(y = f\left( x \right) = {\log _{\frac{1}{{\sqrt 3 }}}}x\). Biết rằng: \(\mathop {\max }\limits_{x \in \left[ {\frac{1}{3};3} \right]} y = M,\mathop {\min }\limits_{x \in \left[ {\frac{1}{3};3} \right]} y = m\). Khi đó:
Với giá trị nào của b thì phương trình \({a^x} = b\left( {a > 0,a \ne 1} \right)\) vô nghiệm?
Nghiệm của phương trình \({\left( {\sqrt 3 } \right)^x} = 3\) là:
Phương trình \({\log _2}x = - 2\) có nghiệm là:
Nghiệm của phương trình \(0,{2^{x - 1}} = \frac{1}{{\sqrt {125} }}\) là:












