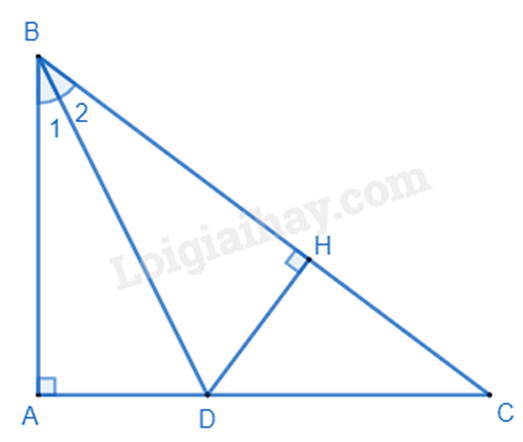
Cho tam giác ABC vuông tại A. Tia phân giác góc B cắt AC tại D. Từ D kẻ DH vuông góc với BC.

a) So sánh BA và BC.

b) Chứng minh DA = DH.

c) So sánh DC và DA.

a) Xét tam giác ABC vuông tại A nên BA là đường vuông góc kẻ từ B đến AC, BC là đường xiên kẻ từ B đến AC nên BA < BC. (quan hệ giữa đường vuông góc và đường xiên).

b) Xét tam giác ABD và HBD, ta có:

$\widehat {BAD} = \widehat {BHD} = {90^0}$

$\widehat {{B_1}} = \widehat {{B_2}}$ (BD là tia phân giác của góc ABC)

BD chung

Suy ra $\Delta ABD = \Delta HBD$ (cạnh huyền – góc nhọn)

Suy ra DA = DH (hai cạnh tương ứng) (đpcm)

c) Trong tam giác DHC có $\widehat {DHC} = {90^0}$

Suy ra DH < DC (cạnh góc vuông nhỏ hơn cạnh huyền)

Mà DA = DH (cmt)

Suy ra DA < DC.