Nội dung từ Loigiaihay.Com
Cho \(\left( {{d_1}} \right):y = x - 4\) và \(\left( {{d_2}} \right):y = - 3x + 2\).
a) Vẽ \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) trên cùng một hệ trục tọa độ.
b) Tìm tọa độ giao điểm của \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\).
c) Tìm m để \(\left( {{d_3}} \right):y = \left( {m - 2} \right)x + 3m + 12\) đi qua giao điểm của \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\).
a) Lấy hai điểm thuộc hàm số để vẽ đồ thị hàm số.
b) Giải phương trình hoành độ giao điểm của hai đường thẳng để tìm tọa độ giao điểm.
c) Thay tọa độ giao điểm của \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) vào \(\left( {{d_3}} \right)\) để tìm m.
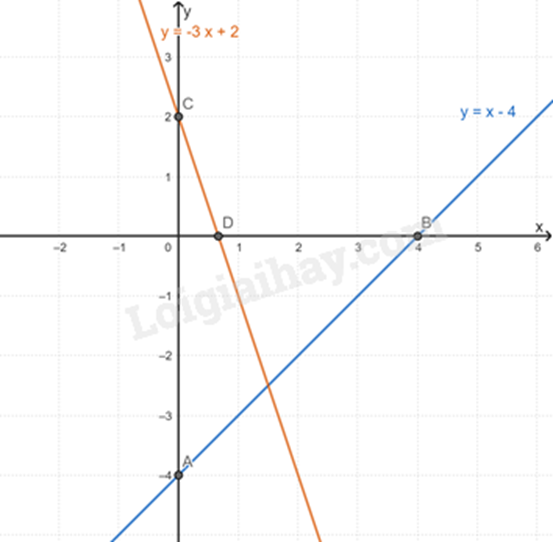
a) Vẽ \(\left( {{d_1}} \right):y = x - 4\)
+ Cho x = 0 thì y = 0 – 4 = -4. Ta được điểm A(0; -4).
+ Cho y = 0 thì 0 = x – 4 => x = 4. Ta được điểm B(4; 0).
Đường thẳng AB chính là đường thẳng \(\left( {{d_1}} \right)\).
Vẽ \(\left( {{d_2}} \right):y = - 3x + 2\)
+ Cho \(x = 0\) thì \(y = - 3.0 + 2 = 2\). Ta được điểm \(C\left( {0;2} \right)\).
+ Cho \(y = 0\) thì \(0 = - 3x + 2 \Rightarrow x = \frac{2}{3}\). Ta được điểm \(D\left( {\frac{2}{3};0} \right)\).
Đường thẳng CD chính là đường thẳng \(\left( {{d_1}} \right)\).
Ta có đường thẳng \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\):
b) Phương trình hoành độ giao điểm của hai đường thẳng là:
\(\begin{array}{l}x - 4 = - 3x + 2\\x + 3x = 2 + 4\\4x = 6\\x = \frac{3}{2}\end{array}\)
\( \Rightarrow y = \frac{3}{2} - 4 = - \frac{5}{2}\).
Vậy tọa độ giao điểm của \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) là \(E\left( {\frac{3}{2};\frac{{ - 5}}{2}} \right)\).
c) Vì \(\left( {{d_3}} \right)\) đi qua tọa độ giao điểm của \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) nên \(E\left( {\frac{3}{2};\frac{{ - 5}}{2}} \right) \in \left( {{d_3}} \right)\).
Thay tọa độ điểm E vào hàm số \(y = \left( {m - 2} \right)x + 3m + 12\), ta được:
\(\begin{array}{l}\frac{{ - 5}}{2} = \left( {m - 2} \right).\frac{3}{2} + 3m + 12\\\frac{{ - 5}}{2} = \frac{3}{2}m - 3 + 3m + 12\\\frac{9}{2}m = - \frac{{23}}{2}\\ \Rightarrow m = - \frac{{23}}{9}\end{array}\)
Vậy \(m = \frac{{ - 23}}{9}\) thì \(\left( {{d_3}} \right):y = \left( {m - 2} \right)x + 3m + 12\) đi qua giao điểm của \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\).

Các bài tập cùng chuyên đề
Trong các hàm số sau hàm số có hệ số góc dương là:
Nếu \(P\left( {1; - 2} \right)\) thuộc đường thẳng \(x - y = m\) thì m bằng:
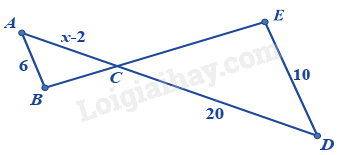
Cho hình vẽ dưới đây, biết AB // DE. Giá trị của x là:
Để đo chiều cao AC của một cột cờ (như hình vẽ), người ta cắm một cái cọc ED có chiều cao 2m vuông góc với mặt đất. Đặt vị trí quan sát tại B, biết khoảng cách BE là 1,5m và khoảng cách AB là 9m.
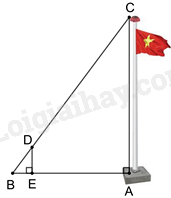
Khi đó chiều cao AC của cột cờ là:
Cho tam giác ABC vuông tại A, biết AB = 3cm, AC = 4cm. Gọi P, Q lần lượt là trung điểm của AB, AC. Khi đó độ dài PQ là:
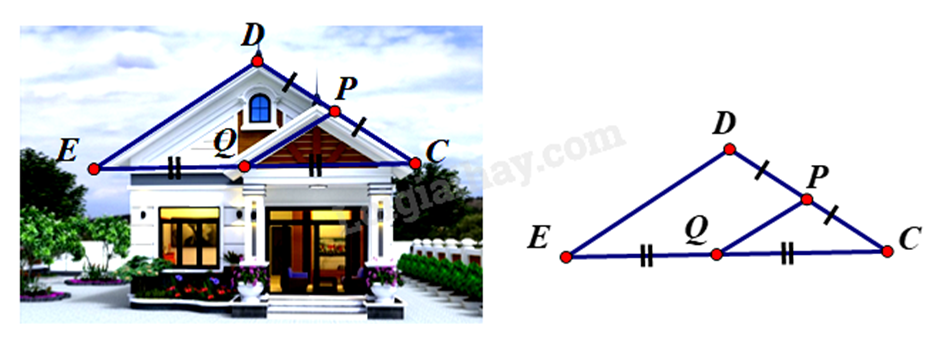
Để thiết kế mặt tiền cho căn nhà cấp bốn mái thái, sau khi xác định chiều dài mái PQ = 1,5m. Chú thợ nhẩm tính chiều dài mái DE biết Q là trung điểm EC, P là trung điểm của DC. Em hãy tính giúp chú thợ xem chiều dài mái DE bằng bao nhiêu (xem hình vẽ minh họa)?
Cho hình thang ABCD (AB // CD). Gọi giao điểm hai đường chéo AC và BD là O. Biết OA = 4cm; OC = 8cm; AB = 5cm.
a) Tính CD.
b) Qua O kẻ đường thẳng vuông góc với AB và CD lần lượt tại H và K. Tính diện tích tam giác AOB, biết OK = 6cm.
c) Qua O kẻ đường thẳng song song với AB cắt AD và BC lần lượt tại E và F. Chứng minh rằng \(OE = OF\).
d) Chứng minh rằng \(\frac{{AE}}{{AD}} + \frac{{CF}}{{BC}} = 1\).
Cho đường thẳng \(\left( {{d_1}} \right):y = ax + b\) song song với đường thẳng \(\left( {{d_2}} \right):y = 2x + 2019\) và cắt trục tung tại điểm \(A\left( {0; - 2} \right)\). Tính giá trị của biểu thức \({a^2} + {b^3}\)?












