Nội dung từ Loigiaihay.Com
1. Một vườn cây có \({x^2} + 2x - {y^2} - 2y\) cây, trong đó có \({x^2} - {y^2}\) cây lấy gỗ còn lại là cây ăn quả.
a) Viết phân thức biểu thị tỉ số cây lấy gỗ và số cây ăn quả.
b) Tính giá trị của phân thức đó tại \(x = 100;y = 10\).
2. Thực hiện phép tính:
a) \(\frac{{1 - 3x}}{{2x}} + \frac{{3x - 2}}{{2x - 1}} + \frac{{3x - 2}}{{2x - 4{x^2}}}\)
b) \(\frac{{{x^2} + x}}{{5{x^2} - 10x + 5}}:\frac{{3x + 3}}{{5x - 5}}\)
1. Sử dụng quy tắc trừ đa thức để tính số cây ăn quả.
a) Viết phân thức có số cây lấy gỗ là tử và số cây ăn quả là mẫu.
b) Thay x = 100 và y = 10 vào phân thức để tính giá trị.
2. Sử dụng các quy tắc tính với phân thức để tính.
1. Số cây ăn quả là:
\(\begin{array}{l}{x^2} + 2x - {y^2} - 2y - \left( {{x^2} - {y^2}} \right)\\ = {x^2} + 2x - {y^2} - 2y - {x^2} + {y^2}\\ = \left( {{x^2} - {x^2}} \right) + \left( { - {y^2} + {y^2}} \right) + 2x - 2y\\ = 2x - 2y\end{array}\)
a) Phân thức biểu thị tỉ số cây lấy gỗ và số cây ăn quả là: \(\frac{{{x^2} - {y^2}}}{{2x - 2y}}\).
b) Ta có: \(\frac{{{x^2} - {y^2}}}{{2x - 2y}} = \frac{{\left( {x - y} \right)\left( {x + y} \right)}}{{2\left( {x - y} \right)}} = \frac{{x + y}}{2}\).
Thay \(x = 100;y = 10\) vào phân thức ta được: \(\frac{{100 + 10}}{2} = \frac{{110}}{2}\).
2.
a) \(\frac{{1 - 3x}}{{2x}} + \frac{{3x - 2}}{{2x - 1}} + \frac{{3x - 2}}{{2x - 4{x^2}}}\) (ĐK: \(x \ne 0;x \ne \frac{1}{2}\))
\(\begin{array}{l} = \frac{{1 - 3x}}{{2x}} + \frac{{3x - 2}}{{2x - 1}} + \frac{{3x - 2}}{{2x\left( {1 - 2x} \right)}}\\ = \frac{{\left( {1 - 3x} \right)\left( {1 - 2x} \right)}}{{2x\left( {1 - 2x} \right)}} - \frac{{2x\left( {3x - 2} \right)}}{{2x\left( {1 - 2x} \right)}} + \frac{{3x - 2}}{{2x\left( {1 - 2x} \right)}}\\ = \frac{{1 - 5x + 6{x^2} - 6{x^2} + 4x + 3x - 2}}{{2x\left( {1 - 2x} \right)}}\\ = \frac{{2x - 1}}{{2x\left( {1 - 2x} \right)}}\\ = \frac{{ - 1}}{{2x}}\end{array}\)
b) \(\frac{{{x^2} + x}}{{5{x^2} - 10x + 5}}:\frac{{3x + 3}}{{5x - 5}}\) (ĐK: \(x \ne 1\))
\(\begin{array}{l} = \frac{{x\left( {x + 1} \right)}}{{5\left( {{x^2} - 2x + 1} \right)}}.\frac{{5\left( {x - 1} \right)}}{{3\left( {x + 1} \right)}}\\ = \frac{{x\left( {x + 1} \right).5\left( {x - 1} \right)}}{{5{{\left( {x - 1} \right)}^2}.3\left( {x + 1} \right)}}\\ = \frac{x}{{3\left( {x - 1} \right)}}\end{array}\)

Các bài tập cùng chuyên đề
Phân thức \(\frac{2}{{x - 3}}\) không có nghĩa khi:
Cho \(\frac{{{{\left( {x + y} \right)}^2}}}{{x - y}} = \frac{P}{{{x^2} - {y^2}}}\). Đa thức P là:
Rút gọn phân thức \(\frac{{{x^3} - 2{x^2}}}{{2{x^2} - 4x}}\) ta được
Thương của hai phân thức \(\frac{{2x}}{{x - 3}}\) và \(\frac{{4{x^2}}}{{3 - x}}\) là:
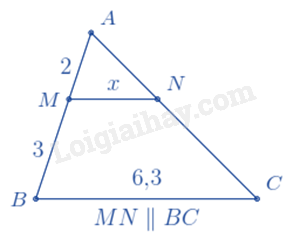
Cho hình vẽ sau, giá trị của x là:
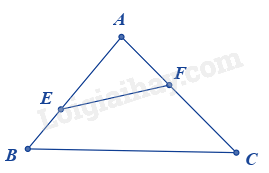
Cho ABC có AB = 24cm, AC = 30cm, BC = 36cm . Trên cạnh AB lấy E sao cho AE = 20cm . Trên cạnh AC lấy F sao cho AF = 16cm. Độ dài cạnh EF là
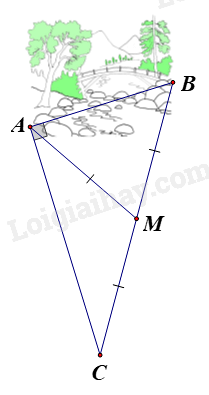
Ông An có một khu vườn, trong đó có miếng đất dạng hình tam giác vuông ABC như hình vẽ bên. Biết M là trung điểm của BC; AC = 40m; AM = 25m. Ông muốn trang trí lại khu vườn của mình nên cần biết khoảng cách từ A đến B. Em hãy giúp ông tính khoảng cách từ A đến B.
Cho $\Delta ABC\backsim \Delta HIK$, biết \(\widehat A = {80^0},\widehat B = {25^0}\). Khi đó số đo \(\widehat K\) bằng
Cho các biểu thức \(P = \frac{1}{{x + 5}} + \frac{2}{{x - 5}} - \frac{{2x + 10}}{{\left( {x + 5} \right)\left( {x - 5} \right)}}\); \(Q = \frac{{x - 4}}{{{x^2} - 25}}\) với \(x \ne \pm 5\).
a) Tính giá trị Q với \(x = 6\).
b) Rút gọn biểu thức P.
c) Đặt \(A = \frac{Q}{P}\). Tìm các giá trị nguyên của x để A nhận giá trị nguyên.
Cho hình vẽ bên. Tính chiều dài của cánh buồm?

(Làm tròn đến hàng phần trăm).
Cho tam giác ABC có ba góc nhọn. Đường cao AF, BE cắt nhau tại H. Từ A kẻ tia Ax vuông góc với AC, từ B kẻ tia By vuông góc với BC. Tia Ax và By cắt nhau tại K.
a) Tứ giác AHBK là hình gì? Vì sao?
b) Chứng minh $\Delta HAE\backsim \Delta HBF$.
c) Chứng minh \(CE.CA = CF.CB\).
d) \(\Delta ABC\) cần thêm điều kiện gì để tứ giác AHBK là hình thoi.
Cho a, b, c và x, y, z là các số khác nhau và khác 0. Chứng minh rằng:
Nếu \(\frac{a}{x} + \frac{b}{y} + \frac{c}{z} = 0\) và \(\frac{x}{a} + \frac{y}{b} + \frac{z}{c} = 1\) thì \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} + \frac{{{z^2}}}{{{c^2}}} = 1\).












