Nội dung từ Loigiaihay.Com
Đề bài
Cho tam giác ABC vuông tại A (AB > AC), đường cao AH. Từ B kẻ tia \(Bx \bot AB\), tia Bx cắt AH tại K.
a) Tứ giác ABKC là hình gì? Tại sao?
b) Chứng minh $\Delta ABK\backsim \Delta CHA$. Từ đó suy ra \(AB.AC = AK.CH\).
c) Chứng minh \(A{H^2} = HB.HC\).
d) Giả sử \(BH = 9cm,HC = 16cm\). Tính AB, AH.
Phương pháp giải
a) Chứng minh tứ giác ABKC có hai cạnh đối song song nên là hình thang và có một góc vuông nên là hình thang vuông.
b) Chứng minh $\Delta ABK\backsim \Delta CHA\left( g.g \right)$ suy ra tỉ số giữa các cạnh trong hai tam giác để chứng minh $AB.AC=AK.CH$.
c) Chứng minh $\Delta AHB\backsim \Delta CHA\left( g.g \right)$ để chứng minh $A{{H}^{2}}=HB.HC$.
d) Áp dụng $A{{H}^{2}}=HB.HC$ để tính AH, định lí Pythagore để tính AB.
Lời giải của GV HocTot.Nam.Name.Vn
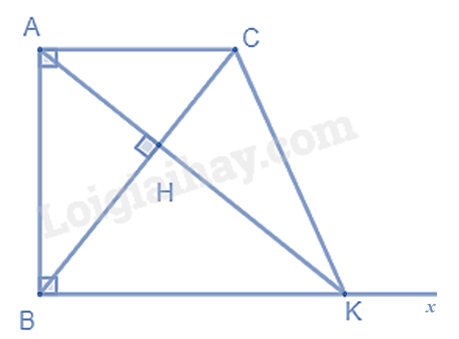
a) Ta có: \(AC \bot AB\left( {gt} \right),BK \bot AB\left( {gt} \right)\) \( \Rightarrow AC//BK\) nên tứ giác ABKC là hình thang.
Mà \(\widehat A = \widehat B = {90^0}\) nên ABKC là hình thang vuông.
b) Vì AC // BK nên \(\widehat {CAH} = \widehat {AKB}\) (hai góc so le trong)
Xét \(\Delta ABK\) và \(\Delta CHA\) có:
\(\widehat B = \widehat H\left( { = {{90}^0}} \right)\)
\(\widehat {CAH} = \widehat {AKB}\) (cmt)
$\Rightarrow \Delta ABK\backsim \Delta CHA\left( g.g \right)$ (đpcm)
\( \Rightarrow \frac{{AB}}{{AK}} = \frac{{CH}}{{CA}} \Rightarrow AB.CA = AK.CH\) (đpcm)
c) Ta có:
\(\left. \begin{array}{l}\widehat {HAC} + \widehat {ACH} = {90^0}\\\widehat {ABC} + \widehat {ACH} = {90^0}\end{array} \right\} \Rightarrow \widehat {HAC} = \widehat {ABC}\)
Xét \(\Delta AHB\) và \(\Delta CHA\) có:
\(\widehat {AHB} = \widehat {CHA}\left( { = {{90}^0}} \right)\)
\(\widehat {HAC} = \widehat {ABC}\)
$\Rightarrow \Delta AHB\backsim \Delta CHA\left( g.g \right)$
\( \Rightarrow \frac{{AH}}{{BH}} = \frac{{CH}}{{AH}} \Rightarrow A{H^2} = BH.CH\) (đpcm)
d) Ta có: \(A{H^2} = BH.CH = 9.16 = 144 = {12^2}\)
\( \Rightarrow AH = 12\left( {cm} \right)\)
Áp dụng định lí Pythagore vào tam giác vuông AHB, ta có:
\(\begin{array}{l}A{B^2} = A{H^2} + H{B^2} = {12^2} + {9^2} = 225\\ \Rightarrow AB = 15\left( {cm} \right)\end{array}\)
Vậy AH = 12cm, AB = 15cm.
Các bài tập cùng chuyên đề
Bài 1 :
Phân thức bằng với phân thức \(\frac{x}{{x - 1}}\) là:
Xem lời giải >>
Bài 2 :
Phân thức nghịch đảo của phân thức \(\frac{{x - y}}{{x + y}}\) là:
Xem lời giải >>
Bài 3 :
Giá trị của phân thức \(\frac{{{x^2} + 4x + 4}}{{{x^2} + 2x}}\) khi \(x = - 2\) là:
Xem lời giải >>
Bài 4 :
Kết quả phép tính \(\frac{{x + 1}}{{x - 1}} - \frac{{x - 4}}{{x - 1}}\) là
Xem lời giải >>
Bài 5 :
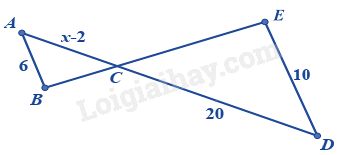
Cho hình vẽ dưới đây, biết AB // DE. Giá trị của x là:
Xem lời giải >>
Bài 6 :
Cho tam giác ABC vuông tại A. Gọi M là trung điểm của AB, N là trung điểm của BC. Biết AB = 3cm, BC = 5cm. Khi đó MN bằng:
Xem lời giải >>
Bài 7 :
Một sân chơi có hình tam giác như hình dưới. Kích thước ba cạnh của sân lần lượt là 300m, 350m và 550m. Phía ngoài sân chơi có một con đường tạo thành một tam giác đồng dạng với sân chơi. Biết cạnh ngắn nhất của con đường là 450m. Tổng chiều dài của con đường đó là:
Xem lời giải >>
Bài 8 :
Cho $\Delta ABC\backsim \Delta MNP$ theo tỉ số đồng dạng 3. Gọi H, K lần lượt là trung điểm của AC, MP. Tỉ số \(\frac{{BH}}{{NK}}\) bằng
Xem lời giải >>
Bài 9 :
Thực hiện phép tính:
a) \(\frac{1}{{x + 1}} + \frac{2}{{1 - x}} + \frac{{5x - 1}}{{{x^2} - 1}}\)
b) \(\frac{{2x + 6}}{{{x^3} - 8}}:\frac{{{{\left( {x + 3} \right)}^3}}}{{2x - 4}}\)
Xem lời giải >>
Bài 10 :
Cho hai biểu thức \(P = \frac{{{x^2} - 2}}{{{x^2} + 2x}} + \frac{1}{{x + 2}}\), \(Q = \frac{{x + 1}}{x}\) (với \(x \ne 0\); \(x \ne - 2\); \(x \ne - 1\))
a) Tính giá trị của Q khi \(x = - 3\).
b) Rút gọn P.
c) Tìm \(x\) để \(P:Q = \frac{5}{2}\).
d) Tìm \(x\) nguyên để \(P\) có giá trị nguyên.
Xem lời giải >>
Bài 11 :
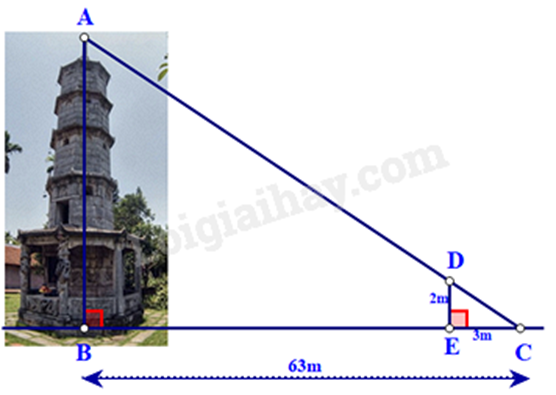
Bóng của một tháp trên mặt đất có độ dài BC = 63m. Cùng thời điểm đó, một cây cột DE cao 2 mét cắm vuông góc với mặt đất có bóng dài 3 mét. Tính chiều cao của tháp?
Xem lời giải >>
Bài 12 :
Chứng minh rằng:
Nếu \(x = by + cz\); \(y = ax + cz\); \(z = ax + by\) và \(x + y + z \ne 0\) thì \(\frac{1}{{1 + a}} + \frac{1}{{1 + b}} + \frac{1}{{1 + c}} = 2\).
Xem lời giải >>