1. Trên giấy kẻ ô vuông (độ dài ô vuông bằng 1cm ), cho tam giác ABC như hình bên. Tính độ dài mỗi cạnh của tam giác ABC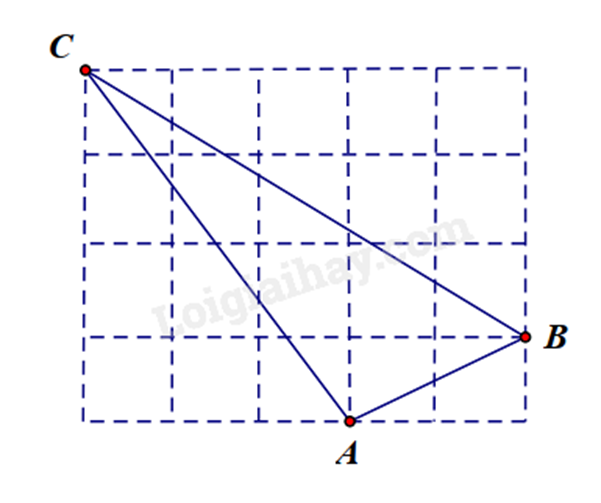

2. Cho tam giác ABC cân tại A, đường trung tuyến AM. Gọi I là trung điểm của AC và K là điểm đối xứng với M qua điểm I.
a) Tứ giác AKCM là hình gì? Vì sao?
b) Chứng minh: AKMB là hình bình hành.
c) Tìm điều kiện của tam giác ABC để tứ giác AKCM là hình vuông.

1. 

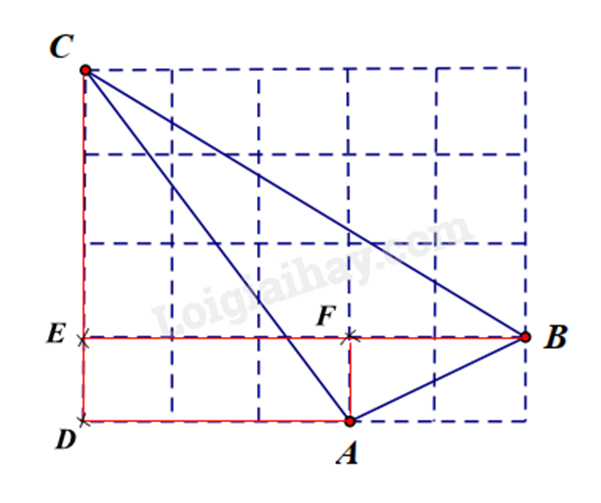
Gọi các điểm D, E và F như trên hình vẽ. Khi đó ta có các tam giác vuông ACD vuông tại D; BCE vuông tại E và ABF vuông tại F.

Tam giác ACD có AD = 3cm; CD = 4cm. Áp dụng định lí Pythagore vào tam giác ADC, ta có:

\(\begin{array}{l}A{C^2} = A{D^2} + C{D^2} = {3^2} + {4^2} = 25\\ \Rightarrow AC = 5cm\end{array}\)

Tam giác BCE có BE = 5cm; CE = 3cm. Áp dụng định lí Pythagore vào tam giác BCE, ta có:

\(\begin{array}{l}B{C^2} = B{E^2} + C{E^2} = {5^2} + {3^2} = 34\\ \Rightarrow BC = \sqrt {34} cm\end{array}\)

Tam giác ABF có AF = 1cm; BF = 2cm. Áp dụng định lí Pythagore vào tam giác ABF, ta có:

\(\begin{array}{l}A{B^2} = A{F^2} + F{B^2} = {1^2} + {2^2} = 5\\ \Rightarrow AB = \sqrt 5 cm\end{array}\)

2. 

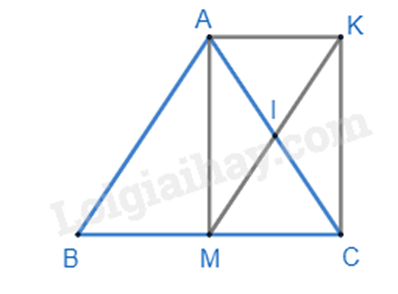
a) Xét tứ giác AKCM có: I là trung điểm của AC; I là trung điểm của KM (vì M đối xứng với K qua I)

=> AKCM là hình bình hành.

Xét tam giác ABC cân tại A có M là trung điểm của BC nên AM là đường trung tuyến đồng thời là đường cao của tam giác ABC. => \(\widehat {AMC} = {90^0}\).

Hình bình hành AKCM có \(\widehat {AMC} = {90^0}\) nên là hình chữ nhật.

b) Ta có AKCM là hình chữ nhật nên AK // CM và AK = CM.

Mà BM = CM nên BM = AK và BM // AK. => Tứ giác AKMB là hình bình hành.

c) Để AKCM là hình chữ nhật thì AM = MC = \(\frac{1}{2}\) Mà AM là đường trung tuyến của tam giác ABC nên khi đó AM là đường trung tuyến ứng với cạnh huyền của tam giác ABC hay tam giác ABC vuông tại A.