Nội dung từ Loigiaihay.Com
Đề bài
Cho biểu thức \(\frac{{{x^2} + \;4x\; + \;4}}{{{x^3} + \;2{x^2} - 4x - 8}}\) (x \( \ne \) \( \pm \) 2)
a) Rút gọn biểu thức.
b) Tìm x \( \in \) Z để A là số nguyên.
Phương pháp giải
a) Sử dụng các phương pháp phân tích đa thức thành nhân tử để rút gọn biểu thức.
b) Để A là số nguyên thì mẫu thức phải là ước của tử thức.
Lời giải của GV HocTot.Nam.Name.Vn
a) Ta có:
\(\begin{array}{l}\frac{{{x^2} + \;4x\; + \;4}}{{{x^3} + \;2{x^2} - 4x - 8}}\\ = \frac{{{{\left( {x + 2} \right)}^2}}}{{{x^2}\left( {x + 2} \right) - 4\left( {x + 2} \right)}}\\ = \frac{{{{\left( {x + 2} \right)}^2}}}{{\left( {{x^2} - 4} \right)\left( {x + 2} \right)}}\\ = \frac{{x + 2}}{{\left( {x - 2} \right)\left( {x + 2} \right)}}\\ = \frac{1}{{x - 2}}\end{array}\)
b) Để A là số nguyên thì \(\frac{1}{{x - 2}} \in \mathbb{Z}\) thì \(x - 2 \in \) Ư(1) \( \Rightarrow x - 2 \in \left\{ { \pm 1} \right\}\).
Ta có: x – 2 = 1 \( \Rightarrow \) x = 3 (thỏa mãn điều kiện)
x – 2 = -1 \( \Rightarrow \) x = 1 (thỏa mãn điều kiện)
Vậy A là số nguyên khi \(x \in \left\{ {1;3} \right\}\).
Các bài tập cùng chuyên đề
Bài 1 :
Một tam giác vuông có độ dài hai cạnh góc vuông lần lượt là 6cm và 8cm thì độ dài đường cao ứng với cạnh huyền là:
Xem lời giải >>
Bài 2 :
Cho hình chóp S.ABCD đều có thể tích bằng 100cm\(^3\), chiều cao SO bằng 12cm. Độ dài cạnh đáy của hình chóp tứ giác đó là :
Xem lời giải >>
Bài 3 :
Cho hình chóp tam giác đều có độ dài cạnh đáy là 5cm, độ dài trung đoạn của hình chóp là 6cm. Diện tích xung quanh của hình chóp tam giác đều đó là :
Xem lời giải >>
Bài 4 :
a) Rút gọn biểu thức \(\frac{{{x^2} + 3xy + \;2{y^2}}}{{{x^3} + \;2{x^2}y - \;x{y^2} - \;2{y^3}}}\) rồi tính giá trị của biểu thức tại x = 5 và y = 3.
b) Phân tích đa thức 2x – 2y – x2 + 2xy – y2 thành nhân tử.
Xem lời giải >>
Bài 5 :
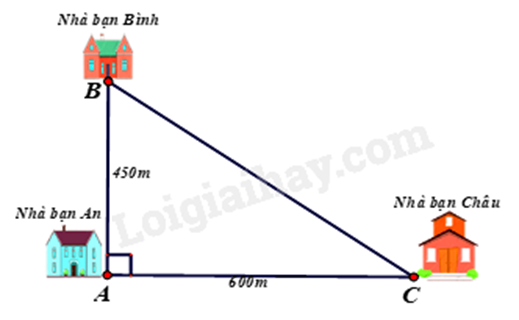
1. Nhà bạn An (vị trí A trên hình vẽ) cách nhà bạn Châu (vị trí C trên hình vẽ) 600m và cách nhà bạn Bình (vị trí B trên hình vẽ) 450m. Biết rằng 3 vị trí: nhà An, nhà Bình và nhà Châu là 3 đỉnh của một tam giác vuông (xem hình vẽ). Hãy tính khoảng cách từ nhà Bình đến nhà Châu.
2. Cho hình thang cân ABCD có DC = 2AB. Gọi M là trung điểm của cạnh DC, N là điểm đối xứng với A qua DC.
a) Chứng minh: Tứ giác ABCM là hình bình hành.
b) Chứng minh: Tứ giác AMND là hình thoi.
c) Khi tứ giác AMND là hình vuông thì góc ABC bằng bao nhiêu?
Xem lời giải >>