Nội dung từ Loigiaihay.Com
Cho hình chữ nhật ABCD có AB=34BC. Hình chữ nhật A’B’C’D’ là hình đồng dạng của hình chữ nhật ABCD theo tỉ số đồng dạng 2. Biết rằng A′C′=10cm. Khi đó, diện tích hình chữ nhật A’B’C’D’ bằng:
-
A.
24cm2
-
B.
48cm2
-
C.
36cm2
-
D.
72cm2
+ Hai hình H, H’ được gọi là đồng dạng nếu có hình H1 đồng dạng phối cảnh với hình H và bằng hình H’
+ Hình H đồng dạng với hình H’ nếu hình H’ bằng H hoặc bằng một hình phóng to hoặc thu nhỏ của H
Vì hình chữ nhật A’B’C’D’ là hình đồng dạng của hình chữ nhật ABCD có tỉ số đồng dạng 2 nên A′B′AB=B′C′BC=2
Mà AB=34BC⇒A′B′=34B′C′.
Vì A’B’C’D’ là hình chữ nhật nên ^A′B′C′=900
Do đó, tam giác A’B’C’ vuông tại B’. Áp dụng định lý Pytago vào tam giác A’B’C’ vuông tại B’ ta có: A′C′2=A′B′2+B′C′2 (1)
Thay A′B′=34B′C′ vào (1) ta có:
(34B′C′)2+B′C′2=102
2516B′C′2=100
B′C′2=64 nên B′C′=8cm
Do đó, A′B′=8.34=6(cm)
Vậy diện tích hình chữ nhật A’B’C’D’ là: A′B′.B′C′=6.8=48(cm2)
Đáp án : B

Các bài tập cùng chuyên đề
Cho hai tam giác ABC và A’B’C’ sao cho 3 đường thẳng AA’, BB’, CC’ cùng đi qua điểm O và OA′OA=OB′OB=OC′OC=3. Khi đó, tam giác ABC và tam giác A’B’C’ là đồng dạng phối cảnh với tỉ số vị tự là:
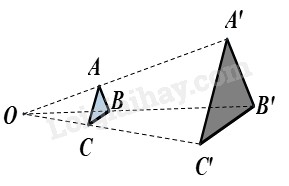
Nếu với mỗi điểm M thuộc hình K, lấy điểm M’ thuộc tia OM sao cho OM′=k.OM thì các điểm M’ đó tạo thành hình K′. Ta nói hình K′ đồng dạng phối cảnh với hình K với tâm phối cảnh là:
Chọn đáp án đúng nhất
Cho hình chữ nhật ba hình chữ nhật ABCD, A’B’C’D’, A”B”C”D” sao cho:
+ Hai hình chữ nhật A”B”C”D” và ABCD là hai hình đồng dạng phối cảnh
+ Hình A”B”C”D” bằng hình A’B’C’D’
Chọn đáp án đúng
Trong những cặp hình cho ở hình vẽ dưới đây, có mấy cặp hình là hình đồng dạng?
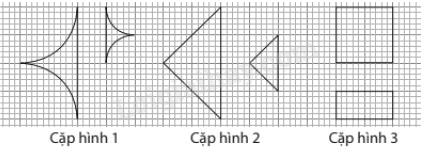
Cho tam giác OAB. Gọi C, D lần lượt là trung điểm của OA và OB.
Chọn đáp án đúng.
Cho các hình vẽ sau:
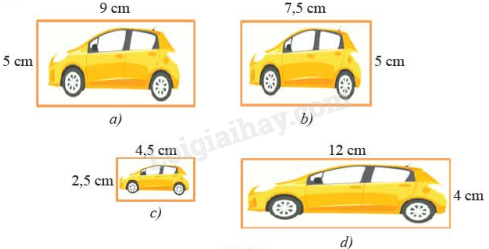
Hình nào đồng dạng với hình a?
Cho đường tròn (O; 6cm) và đường tròn (O; 3cm). Khi đó, đường tròn (O; 6cm) đồng dạng với đường tròn (O; 3cm) theo tỉ số đồng dạng:
Hình vuông A’B’C’D’ là hình vuông ABCD sau khi phóng to với k=3. Nếu độ dài cạnh của hình vuông ABCD là 9cm thì độ dài cạnh của hình vuông A’B’C’D’ là:
Trong hình vẽ bên dưới, các điểm A’, B’, C’, D’ lần lượt là trung điểm của các đoạn thẳng OA, OB, OC, OD.
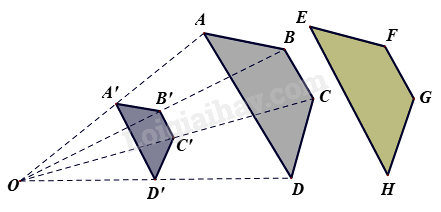
Cho các khẳng định sau:
+ Hình thang ABCD và EFGH bằng nhau
+ Hình thang A’B’C’D và hình thang EFGH đồng dạng với nhau
+ Hình thang ABCD đồng dạng phối cảnh với hình thang A’B’C’D’
Có bao nhiêu khẳng định đúng?
Cho tam giác ABC có AB = 4, BC = 7, CA = 6. Cho O, I là điểm phân biệt.
+ Giả sử tam giác A’B’C’ là hình đồng dạng phối cảnh của tam giác ABC với O là tâm đồng dạng phối cảnh, tỉ số A′B′AB=3
+ Giả sử tam giác A’’B’’C’’ là hình đồng dạng phối cảnh của tam giác ABC với điểm I là tâm đồng dạng phối cảnh, tỉ số A′B′AB=3.
Chọn đáp án đúng
Cho tam giác ABC vuông tại A, gọi M là trung điểm của BC. Qua M vẽ đường thẳng vuông góc với AB cắt AB tại H.
Chọn đáp án đúng
Cho hai hình vuông EFGH, E’F’G’H’ lần lượt có độ dài cạnh là 10cm và 8cm.
Chọn câu trả lời đúng nhất
Tam giác ABC có chu vi bằng 18cm. Tam giác A’B’C’ là hình đồng dạng phối cảnh của tam giác ABC với O là tâm đồng dạng phối cảnh, tỉ số A′B′AB=13. Chu vi tam giác A’B’C’ bằng:
Hình vuông A’B’C’D’ là hình đồng dạng với vuông ABCD theo tỉ số đồng dạng k. Biết rằng diện tích hình vuông A’B’C’D’ bằng 64cm2, diện tích hình vuông ABCD là 36cm2. Khi đó, tỉ số đồng dạng k bằng:
Cho hình tròn H có diện tích bằng 113,04cm2. Hình tròn H’ là hình đồng dạng với hình H có tỉ số đồng dạng bằng 12. Khi đó, diện tích của hình tròn H’ bằng:
Cho tam giác ABC vuông tại A, trên cạnh AB lấy điểm M, trên cạnh AC lấy điểm N sao cho đoạn thẳng MN là hình đồng dạng phối cảnh của đoạn thẳng BC tâm A, tỉ số đồng dạng 14. Biết rằng diện tích tam giác ABC bằng 48cm2. Diện tích tam giác AMN bằng:
Cho tam giác ABC. Trên cạnh BC lấy điểm K sao cho CK=23BC. Tìm trên AB điểm H sao cho cạnh HK là hình đồng dạng phối cảnh của cạnh AC (với tâm đồng dạng phối cảnh là điểm B)
: Cho hình chữ nhật A’B’C’D’ là hình đồng dạng của hình chữ nhật ABCD với tỉ số đồng dạng k. Biết rằng AB=6cm,BC=8cm,A′B′=12cm. Khi đó, diện tích hình chữ nhật A’B’C’D’ là:
Cho tam giác ABC có AB=3cm,BC=4cm,AC=5cm. Tam giác A’B’C’ là hình đồng dạng phối cảnh của tam giác ABC, O là tâm đồng dạng phối cảnh, tỉ số vị tự là 2. Tam giác A”B”C” là hình đồng dạng của tam giác A’B’C’, O là tâm đồng dạng phối cảnh, tỉ số vị tự là x (x>0). Diện tích tam giác A”B”C” bằng 96cm2.
Chọn đáp án đúng












