Nội dung từ Loigiaihay.Com
Cho hình bình hành ABCD. Gọi E, F theo thứ tự là trung điểm của AD, BC. Đường chéo AC cắt BE, DF theo thứ tự ở K, I. Chọn khẳng định đúng nhất.
-
A.
K, I lần lượt là trọng tâm ΔABD, ΔCBD
-
B.
AK = KI = IC
-
C.
Cả A, B đều đúng
-
D.
Cả A, B đều sai
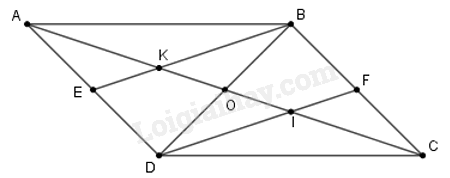
Gọi O là giao điểm của AC, BD
Vì ABCD là hình bình hành nên AC, BD giao nhau tại trung điểm O mỗi đường, hay \(AO = CO = \frac{{AC}}{2}\)
Xét tam giác ABD có BE, AO là đường trung tuyến cắt nhau tại K nên K là trọng tâm ΔABD.
Suy ra \(AK = \frac{2}{3}AO = \frac{2}{3}.\frac{1}{2}AC = \frac{1}{3}AC\) (1)
Xét tam giác CBD có DF, CO là hai đường trung tuyến cắt nhau tại I nên I là trọng tâm ΔCBD.
Suy ra \(CI = \frac{2}{3}CO = \frac{2}{3}.\frac{1}{2}AC = \frac{1}{3}AC\) (2)
Lại có:
\(\begin{array}{l}AK + KI + CI = AC\\ \Rightarrow KI = AC - AK - CI\\ = AC - \frac{1}{3}AC - \frac{1}{2}AC = \frac{1}{3}AC(3)\end{array}\)
Từ (1), (2) và (3) suy ra: AK = KI = IC
Đáp án : C

Các bài tập cùng chuyên đề












