Nội dung từ Loigiaihay.Com
Cho tam giác \(ABC\) vuông cân tại \(A\). Một đường thẳng \(d\) bất kì luôn đi qua \(A\). Kẻ \(BH\) và \(CK\) vuông góc với đường thẳng \(d.\) Khi đó tổng \(B{H^2} + C{K^2}\) bằng
-
A.
\(A{C^2} + B{C^2}\)
-
B.
\(A{H^2}\)
-
C.
\(A{C^2}\)
-
D.
\(B{C^2}\)
+ Chứng minh hai tam giác bằng nhau \(\Delta ABH = \Delta CAK\) suy ra các cạnh tương ứng bằng nhau
+ Sử dụng định lý Py-ta-go
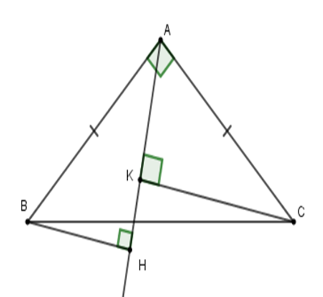
Vì \(\Delta ABC\) vuông cân tại \(A\) nên \(AB = AC\) (tính chất)
Lại có \(\widehat {ABH} + \widehat {BAH} = 90^\circ \) (vì \(\Delta ABH\) vuông tại \(H\) ) và \(\widehat {CAH} + \widehat {BAH} = 90^\circ \)
Nên \(\widehat {ABH} = \widehat {CAK}\) (cùng phụ với \(\widehat {BAH}\) )
\( \Rightarrow \Delta ABH = \Delta CAK\) (cạnh huyền-góc nhọn) suy ra \(BH = AK.\)
Do đó \(B{H^2} + C{K^2} = A{K^2} + C{K^2}\,\,\left( 1 \right)\)
Xét tam giác \(ACK\), theo định lý Pytago: \(A{K^2} + C{K^2} = A{C^2}\,\,\left( 2 \right)\)
Từ (1) và (2) suy ra \(B{H^2} + C{K^2} = A{C^2}.\)
Đáp án : C

Các bài tập cùng chuyên đề
Cho tam giác \(ABC\) và tam giác \(NPM\) có \(BC = PM;\,\widehat B = \widehat P = 90^\circ \). Cần thêm một điều kiện gì để tam giác \(ABC\) và tam giác \(NPM\) bằng nhau theo trường hợp cạnh huyền-cạnh góc vuông ?
Cho tam giác $ABC$ và tam giác $MNP$ có \(\widehat A = \widehat M = {90^0},\,\widehat C = \widehat P\). Cần thêm một điều kiện gì để tam giác $ABC$ và tam giác $MNP$ bằng nhau theo trường hợp cạnh góc vuông – góc nhọn kề:
Cho tam gác $ABC$ và tam giác $DEF$ có \(\widehat B = \widehat E = {90^0},\,AC = DF,\,\,\widehat A = \widehat F\). Phát biểu nào trong các phát biểu sau đây là đúng
Cho tam giác \(ABC\) và tam giác $KHI$ có: \(\widehat A = \widehat K = 90^\circ ;\,AB = KH;\,BC = HI\) . Phát biểu nào trong các phát biểu sau là đúng:
Cho tam giác $ABC$ và tam giác $DEF$ có $AB = DE$ , \(\widehat B = \widehat E\) , \(\widehat A = \widehat D = 90^\circ \). Biết $AC = 9cm.$ Độ dài $DF$ là:
Cho tam giác $DEF$ và tam giác $HKI$ có \(\widehat D = \widehat H = 90^\circ \), \(\widehat E = \widehat K\), $DE = HK.$ Biết \(\widehat F = {80^0}\). Số đo góc \(I\) là:
Cho hình vẽ sau. Chọn câu đúng.
Cho tam giác \(ABC\) có \(M\) là trung điểm của \(BC\) và \(AM\) là tia phân giác của góc \(A\). Khi đó, tam giác \(ABC\) là tam giác gì?
Cho tam giác \(ABC\) vuông cân tại \(A\) và \(D\) là trung điểm \(AC.\) Từ \(A\) kẻ đường vuông góc với \(BD,\) cắt \(BC\) tại \(E.\) Chọn đáp án đúng.