Trong một cuộc thi pha chế, mỗi đội chơi được sử dụng tối đa 24 g hương liệu, 9 lít nước và 210 g đường để pha chế nước cam và nước táo.

• Để pha chế 1 lít nước cam cần 30 g đường, 1 lít nước và 1 g hương liệu;
• Để pha chế 1 lít nước táo cần 10 g đường, 1 lít nước và 4 g hương liệu.

Mỗi lít nước cam nhận được 60 điểm thưởng, mỗi lít nước táo nhận được 80 điểm thưởng. Hỏi cần pha chế bao nhiêu lít nước trái cây mỗi loại để đạt được số điểm thưởng cao nhất?

Giả sử \(x,{\rm{ }}y\) lần lượt là số lít nước cam và số lít nước táo mà mỗi đội cần pha chế.

Suy ra \(30x + 10y\) là số gam đường cần dùng;

  \(x + y\) là số lít nước cần dùng;

  \(x + 4y\) là số gam hương liệu cần dùng.

Theo giả thiết ta có \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\30x + 10y \le 210\\x + y \le 9\\x + 4y \le 24\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge 0\\y \ge 0\\3x + y \le 21\\x + y \le 9\\x + 4y \le 24\end{array} \right..\) \(\left( * \right)\)

Số điểm thưởng nhận được sẽ là \(P = 60x + 80y.\)

Ta đi tìm giá trị lớn nhất của biểu thức \(P\) với \(x,{\rm{ }}y\) thỏa mãn \(\left( * \right)\).

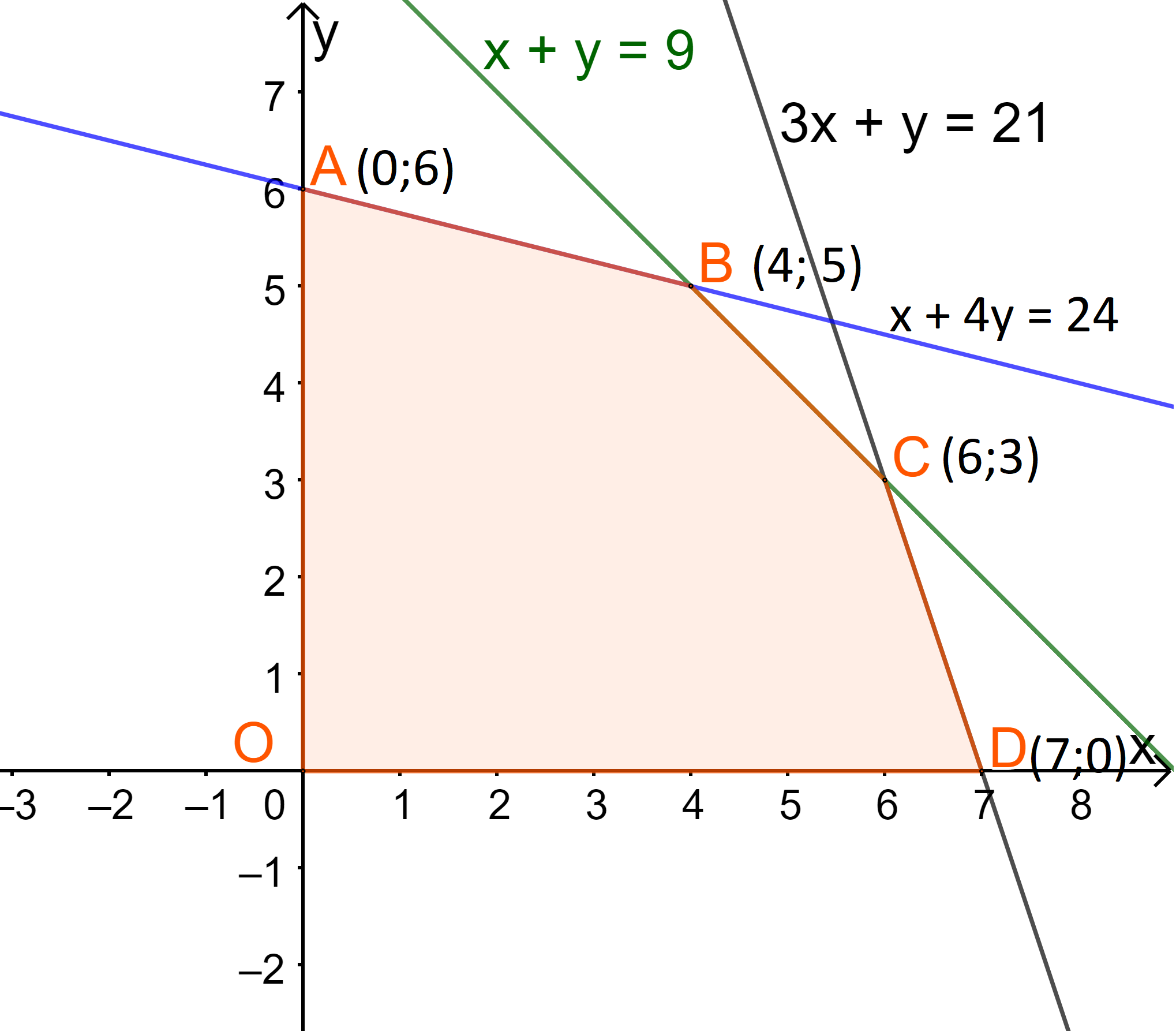
Ta có: 

\(\left\{ {\begin{array}{*{20}{l}}
{60.0 + 80.0 = 0}\\
{60.0 + 80.6 = 480}\\
{60.4 + 80.5 = 640}\\
{60.6 + 80.3 = 600}\\
{60.7 + 80.0 = 420}
\end{array}} \right.\)

Vậy GTLN là 640 tại \(x=4; y= 5\).