Nội dung từ Loigiaihay.Com
Đề bài
Cho ΔABC có AB>AC . Kẻ BN là tia phân giác của góc B (N∈AC). Kẻ CM là tia phân giác của góc C(M∈AB), CM và BN cắt nhau tại I. So sánh IC và IB?
-
A.
IB<IC
-
B.
IC>IB
-
C.
IB=IC
-
D.
IB>IC
Phương pháp giải
- Áp dụng tính chất tia phân giác của một góc.
- Chứng minh ^MCB>^NBC .
- Áp dụng định lý: Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn.
Lời giải của GV HocTot.Nam.Name.Vn
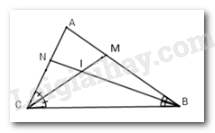
Vì AB>AC⇒^ACB>^ABC(1) (quan hệ giữa cạnh và góc trong tam giác)
Vì BN là phân giác của ^ABC⇒^NBC=^ABC2(2) (tính chất phân giác)
Vì CM là phân giác của ^ACB⇒^MCB=^ACB2(3) (tính chất phân giác)
Từ (1)(2)(3) ⇒^MCB>^NBChay^ICB>^IBC.
Xét ΔBIC có ^MCB>^NBC(cmt)⇒IB>IC (quan hệ giữa góc và cạnh trong tam giác)
Đáp án : D

Các bài tập cùng chuyên đề












