Nội dung từ Loigiaihay.Com
Cho tam giác \(MNP\) có MN = MP. Gọi \(A\) là trung điểm của \(NP.\) Biết \(\widehat {NMA} = {20^0}\) thì số đo góc \(MPN\) là:
-
A.
50\(^\circ \)
-
B.
40\(^\circ \)
-
C.
70\(^\circ \)
-
D.
80\(^\circ \)
+ Áp dụng tính chất hai tam giác bằng nhau suy ra các cặp góc tương ứng bằng nhau.
+ Áp dụng định lý tổng ba góc trong tam giác, tìm góc chưa biết số đo trong tam giác.
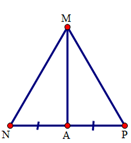
Xét tam giác \(NAM\) và tam giác \(PAM\) có:
\(MN = MP,\) \(NA = PA,\) \(MA\) là cạnh chung.
Do đó \(\Delta NAM = \Delta PAM\,\left( {c - c - c} \right).\)
Nên \(\widehat {ANM} = \widehat {APM}\) ; \(\widehat {NMA} = \widehat {PMA}\) (hai góc tương ứng)
Do đó\(\widehat {NMP} = \widehat {NMA} + \widehat {PMA} = 20^\circ + 20^\circ = 40^\circ \)
Áp dụng định lý tổng 3 góc trong tam giác \(MNP\) có:
\(\widehat {NMP} + \widehat {MPN} + \widehat {PNM} = {180^0} \Rightarrow 2\widehat {MPN} + \widehat {NMP} = {180^0}\)
\(\widehat {MPN} = \left( {{{180}^0} - \widehat {NMP}} \right):2 = \left( {{{180}^0} - {{40}^0}} \right):2 = {70^0}.\)
Đáp án : C

Các bài tập cùng chuyên đề
Cho \(\Delta ABC = \Delta MNP.\) Chọn câu sai.
Cho \(\Delta ABC = \Delta DEF.\) Biết \(\widehat A = {33^0}\). Khi đó
Cho hai tam giác \(ABC\) và \(DEF\) có \(AB = EF;\,BC = FD;AC = ED;\) \(\widehat A = \widehat E;\widehat B = \widehat F;\widehat D = \widehat C\). Khi đó
Cho \(\Delta ABC = \Delta DEF.\) Biết \(\widehat A = {32^0},\widehat F = {78^0}\). Tính \(\widehat B;\widehat E.\)
Cho \(\Delta ABC = \Delta MNP.\) Biết \(AB = 5cm,\) \(MP = 7cm\) và chu vi của tam giác $ABC$ bằng $22cm.$ Tính các cạnh còn lại của mỗi tam giác.
Cho \(\Delta ABC = \Delta DEF.\) Biết rằng \(AB = 6cm,\) \(AC = 8cm\) và \(EF = 10cm.\) Chu vi tam giác \(DEF\) là
Cho \(\Delta ABC = \Delta DEF.\) Biết \(\widehat A + \widehat B = {130^0},\widehat E = {55^0}.\) Tính các góc \(\widehat A,\widehat C,\widehat D,\widehat F.\)
Cho \(\Delta DEF = \Delta MNP.\) Biết \(EF + FD = 10cm,\) \(NP - MP = 2cm,\) \(DE = 3cm.\) Tính độ dài cạnh \(FD.\)
Cho tam giác $ABC$ (không có hai góc nào bằng nhau, không có hai cạnh nào bằng nhau) bằng một tam giác có ba đỉnh là $O,H,K.$ Viết kí hiệu về sự bằng nhau của hai tam giác, biết rằng: \(\widehat A = \widehat O,\widehat B = \widehat K.\)
Cho \(\Delta ABC = \Delta MNP\) trong đó \(\widehat A = 30^\circ ;\widehat P = 60^\circ .\) So sánh các góc \(N;\,M;\,P.\)
Cho hai tam giác $ABD$ và $CDB$ có cạnh chung $BD.$ Biết $AB = DC$ và $AD = CB.$ Phát biểu nào sau đây là sai:
Cho đoạn thẳng \(AB = 6cm.\) Trên một nửa mặt hẳng bờ $AB$ vẽ tam giác $ABC$ sao cho \(AC = 4cm,\) \(BC = 5cm,\) trên nửa mặt phẳng còn lại vẽ tam giác $ABD$ sao cho \(BD = 4cm,\) \(AD = 5cm.\) Chọn câu đúng.
Cho \(\Delta ABC = \Delta DEF.\) Cho \(\widehat E = 46^\circ \). Khẳng định đúng là:
Cho \(\Delta ABC = \Delta MNP.\) Biết AC = 6 cm, NP = 8 cm và chu vi của tam giác MNP bằng 22cm. Tìm khẳng định sai:
Cho hình vẽ sau. Tam giác bằng với tam giác DEA là:
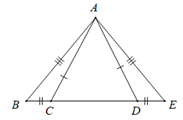
Cho hình dưới đây.
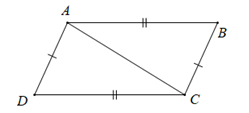
Chọn câu sai.
Cho \(\Delta\)ABC có AB = AC và MB = MC (\(M \in BC\)).Chọn câu sai.
Cho \(\Delta ABC = \Delta DEF.\) Biết \(\widehat A + \widehat B = {130^0},\widehat E = {55^0}.\) Tính các góc \(\widehat A,\widehat C,\widehat D,\widehat F.\)
Cho \(\widehat {xOy} = {50^0}\), vẽ cung tròn tâm O bán kính bằng 2cm, cung tròn này cắt Ox, Oy lần lượt ở A và B. Vẽ các cung tròn tâm A và tâm B có bán kính 3cm, chúng cắt nhau tại điểm C nằm trong góc xOy. Tính \(\widehat {xOC}\) .
Cho hình vẽ sau:
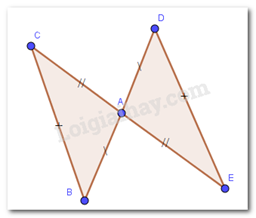
Khẳng định đúng là:












