Nội dung từ Loigiaihay.Com
Cho tập hợp \(A = \{ x \in \mathbb{Q}|({x^2} - 3)(2{x^2} + 5x + 3) = 0\} \). Tập hợp A là:
-
A.
\(A = \{ \sqrt 3 ; - \sqrt 3 ; - 1\} \)
-
B.
\(A = \{ \sqrt 3 ; - \sqrt 3 ; - 1;\frac{{ - 3}}{2}\} \)
-
C.
\(A = \{ \sqrt 3 ; - \sqrt 3 \} \)
-
D.
\(A = \{ - 1;\frac{{ - 3}}{2}\} \)
Cách 1: Dễ thấy: \(A \subset \mathbb{Q}\) nên \(\sqrt 3 \notin A\) (vì \(\sqrt 3 \notin \mathbb{Q}\))
Nên ta loại các đáp án A, B, C => Chọn D.
Cách 2: Ta có:
\(\begin{array}{l}({x^2} - 3)(2{x^2} + 5x + 3) = 0\\ \Leftrightarrow \left[ \begin{array}{l}{x^2} - 3 = 0\\2{x^2} + 5x + 3 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \pm \sqrt 3 \\x = - 1\\x = - \frac{3}{2}\end{array} \right.\end{array}\)
Chỉ lấy các nghiệm \(x = - 1;x = - \frac{3}{2}\) vì \(\sqrt 3 ; - \sqrt 3 \notin \mathbb{Q}\)
\( \Rightarrow A = \{ - 1;\frac{{ - 3}}{2}\} \)
Đáp án : D

Các bài tập cùng chuyên đề
Mô tả tập hợp \(A = \{ x \in \mathbb{Z}| - 1 \le x < 2\} \) bằng cách liệt kê:
Viết lại tập hợp \(B = \{ 0,1,2,3,4,5\} \) bằng cách chỉ ra tính chất đặc trưng.
Kí hiệu nào sau đây để chỉ -2 không là số tự nhiên?
Kí hiệu nào sau đây để chỉ \(\sqrt 2 \) là một số thực nhưng không phải số hữu tỉ?
Chọn đáp án đúng:
Cho \(A = \{ 1;2;3;4;5;6;7;8\} \). Trong các khẳng định sau khẳng định nào sai?
Trong các tập hợp sau, tập nào là tập rỗng?
Cho A là tập hợp các bội của 2, B là tập hợp các bội của 8. Chọn khẳng định đúng:
Cho A là tập hợp các ước của n, B là tập hợp các ước của 12. \((n \in \mathbb{N}*)\)
Điều kiện của n để \(A \subset B\) là:
Số tập con của tập hợp A = {-1;2;b} là
Số tập con có 2 phần tử của tập hợp \(A = \{ a;b;c;d;e;g\} \) là:
Cho tập hợp A biểu thị trên trục số như hình dưới. Chọn khẳng định đúng:
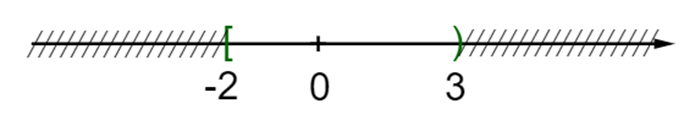
Chọn khẳng định đúng:
Chọn mệnh đề sai:
Tập hợp \(A = (2; + \infty ) \cap [ - 3;8]\) bằng tập hợp nào sau đây?
Tập hợp \(B = (2; + \infty ) \cup [ - 3;8]\) bằng tập hợp nào sau đây?
Tập hợp \(C = (2; + \infty ){\rm{\backslash }}[ - 3;8]\) bằng tập hợp nào sau đây?












