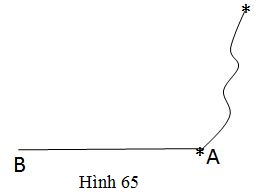
Bài 9 trang 92 SGK Toán 7 tập 2Chứng minh rằng: Nếu tam giác ABC có đường trung tuyến xuất phát từ A bằng một nửa cạnh BC thì tam giác đó vuông tại A. Đề bài Chứng minh rằng: Nếu tam giác ABCABC có đường trung tuyến xuất phát từ AA bằng một nửa cạnh BCBC thì tam giác đó vuông tại A.A. Ứng dụng: Một tờ giấy bị rách ở mép (h.65). Hãy dùng thước và compa dựng đường vuông góc ở cạnh ABAB tại A.A. Video hướng dẫn giải Phương pháp giải - Xem chi tiết - Áp dụng tính chất của tam giác cân. - Áp dụng định lí tổng ba góc trong tam giác. Lời giải chi tiết
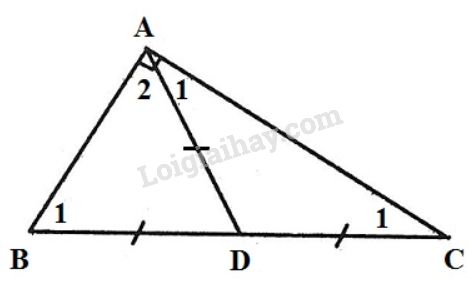
Giả sử ∆ABCΔABC có ADAD là đường trung tuyến ứng với BCBC và AD=12BCAD=12BC. ⇒AD=BD=DC⇒AD=BD=DC. Hay ∆ADC,∆ADBΔADC,ΔADB cùng cân tại DD. Do đó: ^A1=^C1^A2=^B1}⇒^A1+^A2=^B1+^C1 Mà ^A1+^A2+^B1+^C1=^BAC+^B1+^C1=180o (Theo định lí tổng ba góc trong ∆ABC) ⇒ ^A1+^A2=18002=90o Hay ∆ABC vuông tại A. Áp dụng
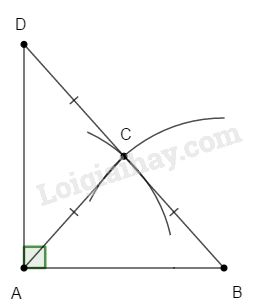
- Vẽ đường tròn (A;r); r>AB2; vẽ đường tròn (B,r) - Gọi C là giao điểm của 2 cung tròn nằm ở phía trong tờ giấy. - Trên tia BC lấy D sao cho BC=CD ⇒AB⊥AD. Thật vậy: ∆ABD có AC là trung tuyến ứng với BD (BD=CD) và AC=BC=CD (theo cách vẽ). ⇒AC=12BD ⇒∆ABD vuông tại A. HocTot.Nam.Name.Vn
|