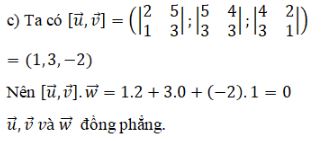Bài 9 trang 81 SGK Hình học 12 Nâng caoXét sự đồng phẳng của ba vectơ trong mỗi trường hợp sau:
Lựa chọn câu để xem lời giải nhanh hơn
Xét sự đồng phẳng của ba vectơ →u,→v và →w trong mỗi trường hợp sau: LG a →u(4;3;4),→v(2;−1;2);→w(1;2;1) Phương pháp giải: Để xét tính đồng phẳng của →u,→v và →w ta xét [→u,→v].→w Nếu [→u,→v].→w=0 thì →u,→v và →w đồng phẳng. Lời giải chi tiết: Ta có: [→u,→v]=(|34−12|;|4422|;|432−1|)=(10;0;−10)⇒[→u,→v].→w=10.1+0.2−10.1=0 Do đó →u,→v,→w đồng phẳng. LG b →u(1;−1;1);→v(0;1;2);→w(4;2;3) Lời giải chi tiết: LG c →u(4;2;5);→v(3;1;3);→w(2;0;1) Lời giải chi tiết: HocTot.Nam.Name.Vn
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
|