Bài 86 trang 51 SBT Hình học 10 Nâng caoGiải bài tập Bài 86 trang 51 SBT Hình học 10 Nâng cao Đề bài Cho tam giác ABC có ˆA=600,a=10,r=5√33. a) Tính R. b) Tính b,c. Lời giải chi tiết
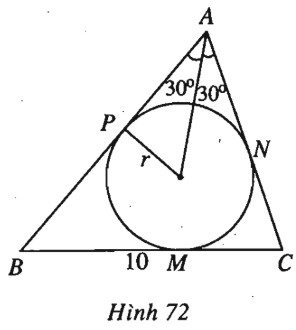
a) Ta có 2R=asinA=10√32=20√33 ⇒R=10√33. b) Gọi M,N,P lần lượt là các tiếp điểm của BC,CA,AB với đường tròn nội tiếp tam giác ABC (h.72). Ta có AP=AN=r.cot300=5; BP+NC=BM+MC=a=10. Từ đó ta có (b−AN)+(c−AP)=10 hay b+c=20. (1) Theo định lí cosin a2=b2+c2−2bccos600 hay a2=(b+c)2−2bc−bc, suy ra bc=(b+c)2−a23 =202−1023=100 (2) Từ (1) và (2) suy ra b,c là nghiệm của phương trình bậc hai x2−20x+100=0. Phương trình này có nghiệm kép b=c=10 nên ABC là tam giác đều. HocTot.Nam.Name.Vn
|