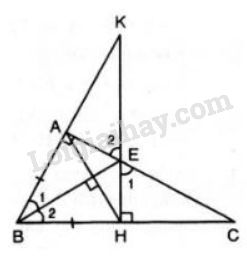
Bài 8 trang 92 SGK Toán 7 tập 2a)∆ABE= ∆HBE. Đề bài Cho tam giác ABC vuông tại A; đường phân giác BE. Kẻ EH vuông góc với BC (H∈BC). Gọi K là giao điểm của AB và HE. Chứng minh rằng: a) ∆ABE=∆HBE. b) BE là đường trung trực của đoạn thẳng AH. c) EK=EC. d) AE<EC. Video hướng dẫn giải Phương pháp giải - Xem chi tiết - Áp dụng tính chất của tia phân giác. - Áp dụng tính chất đường trung trực: các điểm các đều hai mút của đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng đó. - Áp dụng mối quan hệ giữa các cạnh trong tam giác vuông. Lời giải chi tiết
a) Xét hai tam giác vuông ∆ABE và ∆HBE, ta có: +) ^B1=^B2 (do BE là phân giác của góc B) +) BE cạnh huyền chung Vậy ∆ABE=∆HBE (cạnh huyền-góc nhọn) b) Vì ∆ABE=∆HBE (câu a) ⇒BA=BH,EA=EH (hai cạnh tương ứng) ⇒E,B cùng thuộc trung trực của AH nên đường thẳng EB là trung trực của AH. c) Xét ∆AEK và ∆HEC, ta có: +) ^EAK=^EHC=900 +) EA=EH (chứng minh trên) +) ^E2=^E1 (hai góc đối đỉnh) Vậy ∆AEK=∆HEC (g.c.g) ⇒EK=EC (Hai cạnh tương ứng) (điều phải chứng minh) d) Trong tam giác vuông AEK ta có: AE<EK (cạnh huyền lớn hơn cạnh góc vuông) Mà EC=EK (chứng minh trên) Suy ra AE<EC (điều phải chứng minh). HocTot.Nam.Name.Vn
|