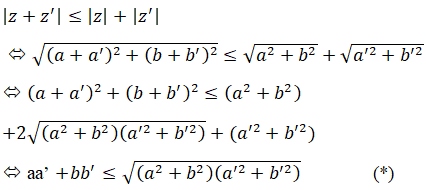Bài 8 trang 190 SGK Giải tích 12 Nâng cao

LG a

Nếu vec tơ \(\overrightarrow u \) của mặt phẳng phức biểu diễn số phức z thì độ dài của vectơ \(\overrightarrow u \) là \(\left| {\overrightarrow u } \right| = \left| z \right|\), và từ đó nếu các điểm \({A_1},{A_2}\) theo thứ tự biểu diễn các số phức \({z_1},{z_2}\) thì \(\left| {\overrightarrow {{A_1}{A_2}} } \right| = |{z_2} - {z_1}|;\)

Phương pháp giải:

Độ dài véc tơ \(\overrightarrow u  = \left( {a;b} \right)\) là \(\left| {\overrightarrow u } \right| = \sqrt {{a^2} + {b^2}} \)

Mô đun số phức \(z = a + bi\) là \(\left| z \right| = \sqrt {{a^2} + {b^2}} \)

Lời giải chi tiết:

Nếu \(z=a+bi\;(a,b\in\mathbb R)\) thì \(|z| = \sqrt {{a^2} + {b^2}} \)

\(\overrightarrow u \) biểu diễn số phức z thì \(\overrightarrow u  = \left( {a;b} \right)\) và \(|\overrightarrow u | = \sqrt {{a^2} + {b^2}} \)

Do đó \(\left| {\overrightarrow u } \right| = \left| z \right|\).

Gọi A₁ là điểm biểu diễn số phức z₁=a₁+b₁ i=>A₁ (a₁;b₁)

A₂ là điểm biểu diễn số phức z₂=a₂+b₂ i=>A₂ (a₂;b₂)

\(\begin{array}{l} \Rightarrow \overrightarrow {{A_1}{A_2}}  = \left( {{a_2} - {a_1};{b_2} - {b_1}} \right)\\ \Rightarrow \left| {\overrightarrow {{A_1}{A_2}} } \right| = \sqrt {{{\left( {{a_2} - {a_1}} \right)}^2} + {{\left( {{b_2} - {b_1}} \right)}^2}} \\{z_2} - {z_1} = \left( {{a_2} + {b_2}i} \right) - \left( {{a_1} + {b_1}i} \right)\\ = \left( {{a_2} - {a_1}} \right) + \left( {{b_2} - {b_1}} \right)i\\ \Rightarrow \left| {{z_2} - {z_1}} \right| = \sqrt {{{\left( {{a_2} - {a_1}} \right)}^2} + {{\left( {{b_2} - {b_1}} \right)}^2}} \\ \Rightarrow \left| {\overrightarrow {{A_1}{A_2}} } \right| = \left| {{z_2} - {z_1}} \right|\end{array}\)

LG b

Với mọi số phức z, z', ta có \(\left| {zz'} \right| = \left| z \right|\left| {z'} \right|\) và khi \(z \ne 0\) thì \(\left| {{{z'} \over z}} \right| = {{|z'|} \over {|z|}};\)

Lời giải chi tiết:

\(z=a+bi;\;z'=a'+b'i\) thì \(|z{|^2} = {a^2} + {b^2};|z'{|^2} = a{'^2} + b{'^2}\) và \(z.z' = (aa' - bb') + (ab' + a'b)i\) nên 

\(\eqalign{
& |z.z'{|^2} = {(aa' - bb')^2} + {(ab' + a'b)^2} \cr & = \left( {aa'} \right) + {\left( {bb'} \right)^2} - 2aa'bb' \cr & + {\left( {ab'} \right)^2} + {\left( {a'b} \right)^2} + 2ab'a'b\cr &= {(aa')^2} + {(bb')^2} + {(ab')^2} + {(a'b)^2} \cr 
&|z{|^2}.|z'{|^2} = \left( {{a^2} + {b^2}} \right)\left( {a{'^2} + b{'^2}} \right)\cr 
& = {a^2}a{'^2} + {a^2}b{'^2} + a{'^2}{b^2} + {b^2}b{'^2}\cr & = {(aa')^2} + {(bb')^2} + {(ab')^2} + {(a'b)^2} \cr 
& \Rightarrow |zz'|^2 = |z|^2.|z'|^2\cr &\Rightarrow |zz'| = |z|.|z'| \cr} \)

Khi \(z \ne 0\) ta có:

\(\left| {{{z'} \over z}} \right| \) \(= \left| {{{z'\overline z } \over {|z{|^2}}}} \right| \) \(= {1 \over {|z{|^2}}}|z'.\overline z | \) \(= {1 \over {|z{|^2}}}.\left| {z'} \right|.\left| {\overline z } \right| \) \(= {1 \over {|z{|^2}}}.|z'|.|z| \) \( = {{|z'|} \over {|z|}}\)

LG c

Với mọi số phức z, z', ta có \(|z + z'| \le |z| + |z'|.\)

Phương pháp giải:

Đưa về véc tơ biểu diễn số phức và áp dụng bất đẳng thức véc tơ suy ra đpcm.

Lời giải chi tiết:

Giả sử \(\overrightarrow u \) biểu diễn z và \(\overrightarrow {u'} \) biểu diễn z' thì \(\overrightarrow u+\overrightarrow {u'} \) biểu diễn z+z'. Ta có:

\(\left| {\overrightarrow u  + \overrightarrow {u'} } \right| = \left| {z + z'} \right|;\,\left| {\overrightarrow u } \right| = \left| z \right|;\) \(\left| {\overrightarrow {u'} } \right| = \left| {z'} \right|\)

Mà \(\left| {\overrightarrow u  + \overrightarrow {u'} } \right| \le \left| {\overrightarrow u } \right| + \left| {\overrightarrow {u'} } \right|\) nên \(\left| {z + z'} \right| \le \left| z \right| + \left| {z'} \right|\)

Dấu "=" xảy ra khi \(z=0\) hoặc \(z'=0\).

Cách khác:

Với mọi số phức z, z’, ta có: z + z’ = (a +a’) + (b +b’)i

\(\begin{array}{l} \Rightarrow \left| {z + z'} \right| = \sqrt {{{\left( {a + a'} \right)}^2} + {{\left( {b + b'} \right)}^2}} \\\left| z \right| + \left| {z'} \right| = \sqrt {{a^2} + {b^2}}  + \sqrt {a{'^2} + b{'^2}} \end{array}\)

Theo yêu cầu bài toán ta cần chứng minh:

Theo Bu-nhi-cốp-xki ta có bất đẳng thức (*) đúng với ∀a,b,a',b'∈R nên |z+z'| ≤ |z|+|z'| (đpcm)

HocTot.Nam.Name.Vn