Bài 8. Chuyển động biến đổi. Gia tốc trang 37, 38, 39 Vật Lí 10 Kết nối tri thứcHãy tìm thêm ví dụ về chuyển động biến đổi trong cuộc sốngXác định độ biến thiên vận tốc sau 8 s của chuyển động trên. Xác định độ biến thiên của vận tốc sau mỗi giây của chuyển động trên trong 4 s đầu và trong 4 s cuối. Các đại lượng xác định được ở câu 2 cho ta biết điều gì về sự thay đổi vận tốc của chuyển động trên. Hãy chứng tỏ khi cùng chiều với (a.v>0) thì chuyển động là nhanh dần, khi ngược chiều với (a.v<0) thì chuyển động là chậm dần). Tính gia tốc của ô tô trên 4 đoạn đường tr Video hướng dẫn giải Câu hỏi tr 37
Phương pháp giải: Liên hệ thực tế Lời giải chi tiết: Ví dụ về chuyển động biến đổi trong cuộc sống: + Máy bay đang bay trên bầu trời + Xe máy đang chuyển động trên đường + Con muỗi đang bay... Câu hỏi tr 38 CH 1
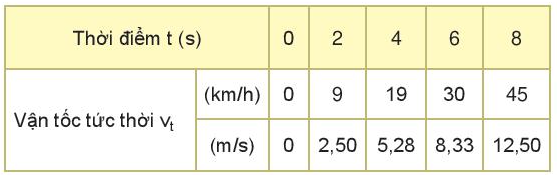
Phương pháp giải: Biểu thức độ biến thiên vận tốc: \(a = \frac{{\Delta v}}{{\Delta t}}\) Lời giải chi tiết: 1. Bảng số liệu của chuyển động
Độ biến thiên vận tốc sau 8 s là: \(a = \frac{{\Delta v}}{{\Delta t}} = \frac{{12,5}}{8} = 1,5625(m/{s^2})\) 2. Độ biến thiên vận tốc sau 4 s đầu chuyển động: \(a = \frac{{\Delta {v_4}}}{{\Delta {t_4}}} = \frac{{5,28}}{4} = 1,32(m/{s^2})\) + Độ biến thiên vận tốc sau 4 s sau chuyển động: \(a = \frac{{\Delta v}}{{\Delta t}} = \frac{{12,50 - 5,28}}{4} = 1,805(m/{s^2})\) 3. Các đại lượng được xác định trong câu 2 cho ta biết vận tốc của vật chuyển động tăng dần. Câu hỏi tr 38 CH 2
Phương pháp giải: Gia tốc a cho biết sự thay đổi nhanh chậm của vận tốc. Lời giải chi tiết: + Chọn chiều dương là chiều chuyển động của vật + Giả sử vật chuyển động theo chiều dương nên v >0 + Khi vật chuyển động nhanh dần thì vận tốc của vật cũng tăng dần, nên theo biểu thức tính gia tốc \(a = \frac{{\Delta v}}{{\Delta t}}\) , \(\Delta v > 0\) => a.v>0 + Khi vật chuyển động chậm dần thì vận tốc giảm dần, \(\Delta v < 0\) => a.v<0 Câu hỏi tr 39
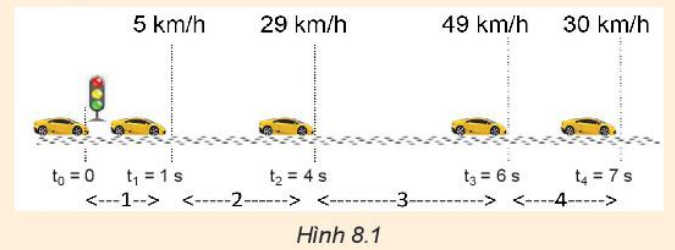
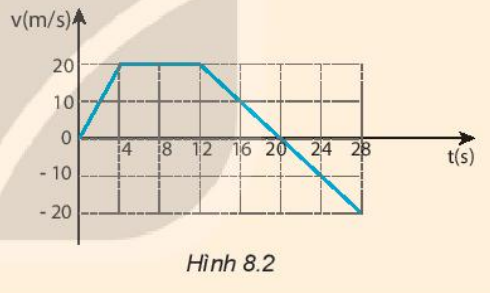
Phương pháp giải: + Biểu thức tính gia tốc: \(a = \frac{{\Delta v}}{{\Delta t}}\) + 1 m/s = 3,6 km/h Lời giải chi tiết: 1. a) Đổi 5 km/h = \(\frac{{25}}{{18}}\)m/s; 29 km/h = \(\frac{{145}}{{18}}\)m/s; 49 km/h = \(\frac{{245}}{{18}}\); 30 km/h = \(\frac{{25}}{3}\)m/s + Gia tốc trong đoạn đường 1: \(a = \frac{{\Delta v}}{{\Delta t}} = \frac{{25}}{{18.1}} = \frac{{25}}{{18}} \approx 1,39(m/{s^2})\) + Gia tốc trong đoạn đường 2: \(a = \frac{{\Delta v}}{{\Delta t}} = \frac{{\frac{{145}}{{18}} - \frac{{25}}{{18}}}}{{4 - 1}} \approx 2,22(m/{s^2})\) + Gia tốc trong đoạn đường 3: \(a = \frac{{\Delta v}}{{\Delta t}} = \frac{{\frac{{245}}{{18}} - \frac{{145}}{{18}}}}{{6 - 4}} \approx 2,78(m/{s^2})\) + Gia tốc trong đoạn đường 4: \(a = \frac{{\Delta v}}{{\Delta t}} = \frac{{\frac{{25}}{3} - \frac{{245}}{{18}}}}{{7 - 6}} \approx - 5,28(m/{s^2})\) b) Trong 4 đoạn đường trên, vận tốc tăng dần, còn gia tốc từ đoạn đường 1 đến đoạn đường 3 tăng dần, nhưng từ đoạn đường 3 đến đoạn đường 4 thì gia tốc giảm dần. 2. Gia tốc của con báo là: \(a = \frac{{\Delta v}}{{\Delta t}} = \frac{{9 - 30}}{3} = - 7(m/{s^2})\) 3. a) Trong 4 s đầu: \(\begin{array}{l}\Delta v = 20(m/s);\Delta t = 4(s)\\ \Rightarrow a = \frac{{\Delta v}}{{\Delta t}} = \frac{{20}}{4} = 5(m/{s^2})\end{array}\) b) Từ giây thứ 4 đến giây thứ 12 \(\begin{array}{l}\Delta v = 20 - 20 = 0(m/s);\Delta t = 12 - 4 = 8(s)\\ \Rightarrow a = \frac{{\Delta v}}{{\Delta t}} = 0(m/{s^2})\end{array}\) c) Từ giây thứ 12 đến giây thứ 20: \(\begin{array}{l}\Delta v = 0 - 20 = - 20(m/s);\Delta t = 20 - 12 = 8(s)\\ \Rightarrow a = \frac{{\Delta v}}{{\Delta t}} = \frac{{ - 20}}{8} = - 2,5(m/{s^2})\end{array}\) d) Từ giây thứ 20 đến giây thứ 28: \(\begin{array}{l}\Delta v = - 20 - 0 = - 20(m/s);\Delta t = 28 - 20 = 8(s)\\ \Rightarrow a = \frac{{\Delta v}}{{\Delta t}} = \frac{{ - 20}}{8} = - 2,5(m/{s^2})\end{array}\)  Chia sẻ Bình luận
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
