Bài 74 trang 62 SGK giải tích 12 nâng cao

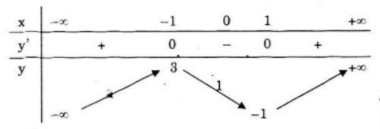
LG a

Khảo sát sự biến thiên và vẽ đồ thị của hàm số.

Lời giải chi tiết:

Tập xác định \(D=\mathbb R\)

\(f'\left( x \right) = 3{x^2} - 3\)

\(f'(x) = 0 \Leftrightarrow \left[ \matrix{
x = 1 \hfill \cr 
x = - 1 \hfill \cr} \right.\)

Hàm số đồng biến trên khoảng: \(\left( { - \infty ; - 1} \right)\) và \( \left( {1; + \infty } \right)\)

 Hàm số nghịch biến trên khoảng \((-1;1)\)

+) Cực trị:

 Hàm số đạt cực đại tại \(x=-1;y(-1)=3\)

 Hàm số đạt cực tiểu tại \(x=1; y(1)=-1\)

+) Giới hạn:

\(\eqalign{
& \mathop {\lim }\limits_{x \to + \infty } f(x) = + \infty \cr 
& \mathop {\lim }\limits_{x \to - \infty } f(x) = - \infty \cr} \)

 Bảng biến thiên:

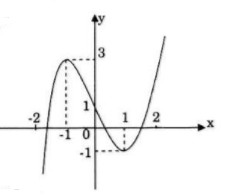
Đồ thị

Đồ thị giao trục \(Oy\) tại điểm \((0;1)\)

Hàm số đồ thị nhận \(I(0;1)\)  làm tâm đối xứng

LG b

Viết phương trình tiếp tuyến của đồ thị tại điểm uốn U của nó.

Lời giải chi tiết:

\(f'\left( x \right) = 3{x^2} - 3\)

\(f''\left( x \right)=6x\)

\(f''\left( x \right) = 0 \Leftrightarrow x = 0; f'(0)=-3\)

\(f\left( 0 \right) = 1\). Điểm uốn U(0;1)

Phương tiếp tuyến của (C) tại U là:

\(y - 1 = f'\left( 0 \right)\left( {x - 0} \right)\) \( \Leftrightarrow y =  - 3x + 1\)

LG c

Gọi \(\left( {{d_m}} \right)\) là đường thẳng đi qua điểm U và có hệ số góc m. Tìm các giá trị của m sao cho đường thẳng \(\left( {{d_m}} \right)\) cắt đồ thị của hàm số đã cho tại ba điểm phân biệt.

Lời giải chi tiết:

Phương trình đường thẳng \(\left( {{d_m}} \right)\) là y = mx +1.

Hoành độ giao điểm của đường thẳng \(\left( {{d_m}} \right)\) và đường cong (C) là nghiệm của phương trình

\({x^3} - 3x + 1 = mx + 1\) \( \Leftrightarrow {x^3} - \left( {m + 3} \right)x = 0\)

\( \Leftrightarrow \left[ \matrix{
x = 0 \hfill \cr 
{x^2} = m + 3 \,\,(2)\hfill \cr} \right.\)

\(\left( {{d_m}} \right)\) cắt (C) tại 3 điểm phân biệt khi và chỉ khi (1) có 3 nghiệm phân biệt

\( \Leftrightarrow \left( 2 \right)\) có hai nghiệm phân biệt khác 0, tức \(m + 3 > 0 \Leftrightarrow m >  - 3\)

Chú ý:

ĐK tổng quát các em có thể dùng: 

(1) có 3 nghiệm phân biệt \( \Leftrightarrow \left( 2 \right)\) có hai nghiệm phân biệt khác 0

\( \Leftrightarrow \left\{ \begin{array}{l}\Delta ' > 0\\f\left( 0 \right) \ne 0\end{array} \right.\)

HocTot.Nam.Name.Vn