Bài 73 trang 62 SGK giải tích 12 nâng cao

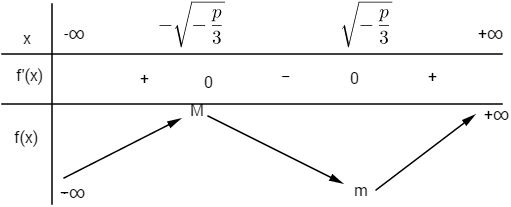
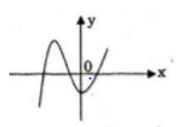
LG a

Tìm điều kiện đối với p và q để hàm số f có một cực đại và một cực tiểu.

Lời giải chi tiết:

Ta có \(f'\left( x \right) = 3{x^2} + p\)

\(f'\left( x \right) = 0 \Leftrightarrow 3{x^2} + p = 0\,\,\left( 1 \right)\)

Hàm số f có một cực đại và một cực tiểu khi và chỉ khi khi phương trình (1) có hai nghiệm phân biệt \( \Leftrightarrow p < 0\)

Chú ý:

Khi làm dạng toán này chỉ cần tìm điều kiện như trên là đủ, dưới đây là kiểm nghiệm lại kết luận, không cần làm vào bài tránh dài dòng.

Khi \(p < 0\), hai nghiệm của (1) là: \(x =  - \sqrt { - {p \over 3}} ;\,\,\,x = \sqrt { - {p \over 3}} \)

Bảng biến thiên: 

Với \(M = {\left( { - \sqrt { - {p \over 3}} } \right)^3} - p\sqrt { - {p \over 3}}  +q\) \(= q - {2 \over 3}p\sqrt { - {p \over 3}} \)

\(m = {\left( {\sqrt { - {p \over 3}} } \right)^3} + p\sqrt { - {p \over 3}}  + q \) \(= q + {2 \over 3}p\sqrt { - {p \over 3}} \)

LG b

Chứng minh rằng nếu giá trị cực đại và giá trị cực tiểu trái dấu thì phương trình: \({x^3} + px + q = 0\,\,\left( 1 \right)\) có ba nghiệm phân biệt.

Lời giải chi tiết:

Cách 1.

Dạng đồ thị như hình vẽ:

Đồ thị cắt trục hoành tại ba điểm phân biệt nên phương trình x³+px+q= 0 có 3 nghiệm phân biệt.

Cách 2.

Hàm số f(x) = x³+px+q liên tục trên R và có

\({f_{CD}}.{f_{CT}} < 0 \Leftrightarrow \left\{ \begin{array}{l}{f_{CD}} > 0\\{f_{CT}} < 0\end{array} \right.\) (vì \(a = 1 > 0\))

f_CĐ=f(x₁ ), f_CT=f(x₂ )

Do \(\mathop {\lim }\limits_{x \to  - \infty } f\left( x \right) =  - \infty \) nên tồn tại số a sao cho f(a) < 0, với a<x₁

Vì f(a).f_CĐ < 0 nên phương trình có ít nhất 1 nghiệm thuộc (a,x₁)

Và f(x₁ ).f(x₂ ) < 0 nên phương trình có ít nhất 1 nghiệm thuộc (x₁,x₂)

Do \(\mathop {\lim }\limits_{x \to  + \infty } f\left( x \right) =  + \infty \) nên tồn tại một số b > x₂ sao cho f(b) > 0

Vì f(x₂ ).f(b) < 0 nên phương trình có ít nhất 1 nghiệm thuộc (x₂,b)

Do phương trình bậc ba có nhiều nhất là 3 nghiệm.

Vậy phương trình x³+px+q=0 có 3 nghiệm phân biệt.

Chú ý: Khẳng định trên đúng với phương trình bậc ba tổng quát.

LG c

Chứng minh rằng điều kiện cần và đủ để phương trình (1) có ba nghiệm phân biệt là: \(4{p^3} + 27{q^2} < 0\)

Lời giải chi tiết:

Điều kiện cần và đủ để phương trình (1) có ba nghiệm phân biệt là: 

\(\left\{ \matrix{
p < 0 \hfill \cr 
Mm < 0 \hfill \cr} \right. \)

\(\begin{array}{l}
\Leftrightarrow \left\{ \begin{array}{l}
p < 0\\
\left( {q - \frac{2}{3}p\sqrt { - \frac{p}{3}} } \right)\left( {q - \frac{2}{3}p\sqrt { - \frac{p}{3}} } \right) < 0
\end{array} \right.\\
\Leftrightarrow \left\{ \begin{array}{l}
p < 0\\
{q^2} - \frac{4}{9}{p^2}\left( { - \frac{p}{3}} \right) < 0
\end{array} \right.\\
\Leftrightarrow \left\{ \begin{array}{l}
p < 0\\
{q^2} + \frac{{4{p^3}}}{{27}} = 0
\end{array} \right.\\
\Leftrightarrow \left\{ \begin{array}{l}
p < 0\\
27{q^2} + 4{p^3} = 0
\end{array} \right.
\end{array}\)

Cách khác:

Gọi x₁,x₂ là hai điểm cực trị của hàm số.

Theo câu b, ta có điều kiện cần và đủ để phương trình (1) có ba nghiệm phân biệt là giá trị cực đại và cực tiểu trái dấu nhau, nghĩa là y_CD.y_CT<0

<=> f(x₁ ).f(x₂ )<0

HocTot.Nam.Name.Vn