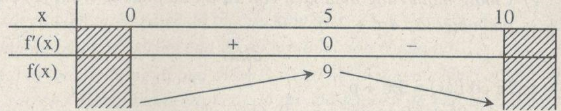Bài 71 trang 62 SGK giải tích 12 nâng cao

Đề bài

Chu vi của một tam giác là 16cm, độ dài một cạnh tam giác là 6cm. Tìm độ dài hai cạnh còn lại của tam giác sao cho tam giác có diện tích lớn nhât.

Lời giải chi tiết

Gọi x, y là độ dài hai cạnh còn lại của tam giác.

Nửa chu vi tam giác là p=16:2=8.

Ta có: \(x + y = 16 - 6 = 10\) \(\Rightarrow y = 10 - x\) với \(x > 0,\,y > 0\)

Diện tích tam giác là:

\(S = \sqrt {p\left( {p - 6} \right)\left( {p - x} \right)\left( {p - y} \right)}  \)

\(= \sqrt {8.2\left( {8 - x} \right)\left( {8 - y} \right)}  \)

\(= 4\sqrt {\left( {8 - x} \right)\left( {8 - y} \right)} \)

Thay y= 10- x , ta được \(S = 4\sqrt {\left( {8 - x} \right)\left( {x - 2} \right)} \)

\(= 4\sqrt {{-x^2} + 10x - 16} \,\,\,\left( {0 < x < 10} \right)\)

S đạt giá trị lớn nhất trên khoảng (0;10) khi và chỉ khi hàm số \(f\left( x \right) =  - {x^2} + 10x - 16\) đạt giá trị lớn nhất trên khoảng (0;10).

\(f'\left( x \right) =  - 2x + 10\)

\(f'\left( x \right) = 0 \Leftrightarrow x = 5;\,f\left( 5 \right) = 9\)

Tam giác có diện tích lớn nhất khi x = 5 (cm) và y= 5 (cm)

\(\mathop {\max }\limits_{x \in \left( {0;10} \right)} f\left( x \right) = f\left( 5 \right) = 9\)

Khi đó diện tích tam giác là: \(S = 4\sqrt {(8-5)(5-2)}  = 12\left( {c{m^2}} \right)\)

Cách khác:

Ta có: \(S = 4\sqrt {\left( {8 - x} \right)\left( {x - 2} \right)} \)

ĐK: \(\left( {8 - x} \right)\left( {x - 2} \right) \ge 0 \) \(\Leftrightarrow 2 \le x \le 8\)

Áp dụng BĐT Cô - si cho hai số không âm \(a=8-x\) và \(b=x-2\) ta có:

\(\begin{array}{l}
\sqrt {\left( {8 - x} \right)\left( {x - 2} \right)} \le \frac{{8 - x + x - 2}}{2} = 3\\
\Rightarrow S \le 4.3 = 12
\end{array}\)

Dấu "=" xảy ra khi \(8 - x = x - 2 \)

\(\Leftrightarrow 10 = 2x \Leftrightarrow x = 5\).

HocTot.Nam.Name.Vn