Bài 7 trang 45 SGK Hình học 12 Nâng cao

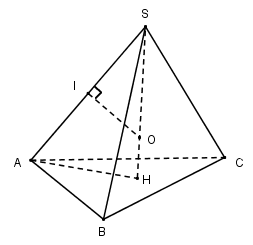
LG a

Tính thể tích khối cầu ngoại tiếp hình chóp tam giác đều có cạnh đáy bằng \(a\) và chiều cao bằng \(h\).

Lời giải chi tiết:

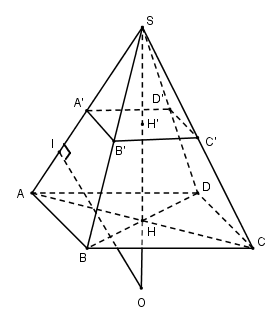
Gọi \(H\) là tâm của tam giác đều \(ABC\).

\(SH\) là đường cao của hình chóp đều \(S.ABC\) nên \(SH\) là trục của tam giác \(ABC\).

Trong mặt phẳng \((SAH)\) gọi \(O\) là giao điểm của đường trung trực \(SA\) với \(SH\) thì \(O\) là tâm của mặt cầu ngoại tiếp hình chóp và bán kính của mặt cầu là \(R = SO\).

Gọi \(I\) là trung điểm của \(SA\) thì tứ giác \(AHOI\) nội tiếp nên:

\(SO.SH = SI.SA\) \( \Rightarrow SO = {{S{A^2}} \over {2SH}} = {{S{A^2}} \over {2h}}\)

Mà \(S{A^2} = S{H^2} + A{H^2} \) \( = {h^2} + {\left( {{{a\sqrt 3 } \over 3}} \right)^2} = {{{a^2} + 3{h^2}} \over 3}\)

Từ đó suy ra \(R = SO = {{{a^2} + 3{h^2}} \over {6h}}\)

Vậy thể tích khối cầu cần tìm là \(V = {{\pi {{\left( {{a^2} + 3{h^2}} \right)}^3}} \over {162{h^3}}}\)

LG b

Cho hình chóp tứ giác đều \(S.ABCD\) có tất cả các cạnh cùng bằng \(a\). Gọi \(A’, B’, C’, D’\) lần lượt là trung điểm của \(SA, SB, SC, SD\). Chứng minh rằng các điểm \(A, B, C, D, A’, B’, C’, D’\) cùng thuộc một mặt cầu và tính thể tích khối cầu đó.

Lời giải chi tiết:

Gọi \(SH\) là đường cao của hình chóp đều \(S.ABCD\) thì \(H\) là tâm của hình vuông \(ABCD\) và \(SH\) đi qua tâm \(H’\) của hình vuông \(A’B’C’D’\).

Mọi điểm nằm trên \(SH\) đều cách đều bốn điểm \(A’, B’, C’, D’\).

Trên đường thẳng \(SH\), ta xác định điểm \(O\) sao cho \(OA = OA’\) thì \(O\) cách đều tám điểm \(A, B, C, D, A’, B’, C’, D’\) tức là tám điểm đó nằm trên mặt cầu tâm \(O\), bán kính \(R = OA\).

Điểm \(O\) là giao điểm của đường thẳng \(SH\) và mặt phẳng trung trực của đoạn thẳng \(AA’\).

Ta có: \(2{a^2} = A{C^2} = S{A^2} + S{C^2}\) nên tam giác vuông cân tại S suy ra \(\widehat {ASO} = {45^0}\) do đó ASIO vuông cân tại I và \(IS = IO = {{3a} \over 4}\).

Từ đó suy ra \(R = OA = \sqrt {O{I^2} + I{A^2}} \) \( = \sqrt {{{9{a^2}} \over {16}} + {{{a^2}} \over {16}}}  = {{a\sqrt {10} } \over 4}\)

Vậy thể tích khối cầu cần tìm là: \(V = {4 \over 3}\pi {\left( {{{a\sqrt {10} } \over 4}} \right)^3} = {{5\pi {a^3}\sqrt {10} } \over {24}}\)

HocTot.Nam.Name.Vn