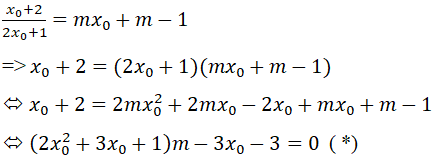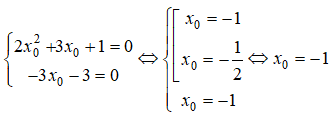Bài 63 trang 57 SGK giải tích 12 nâng cao

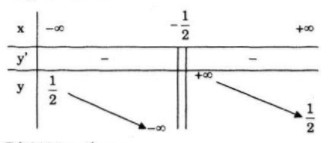
LG a

Khảo sát sự biến thiên và vẽ đồ thị \((H)\) của hàm số: \(y = {{x + 2} \over {2x + 1}}\)

Lời giải chi tiết:

Tập xác định: \(D =\mathbb R\backslash \left\{ { - {1 \over 2}} \right\}\)

+) Sự biến thiên:

\(y' = {{ - 3} \over {{{(2x + 1)}^2}}} < 0\,\forall x \in D\)

Hàm số nghịch biến trên khoảng \(\left( { - \infty ; - {1 \over 2}} \right)\) và \(\left( { - {1 \over 2}; + \infty } \right)\)

Giới hạn:

\(\mathop {\lim y}\limits_{x \to  - {{{1 \over 2}}^ - }}  =  - \infty ;\,\mathop {\lim y}\limits_{x \to  - {{{1 \over 2}}^ + }}  =  + \infty \)

Hầm số không có cực trị.

Tiệm cận đứng: \(x={ - {1 \over 2}}\)

\(\mathop {\lim y}\limits_{x \to  \pm \infty }  = {1 \over 2}\)

Tiệm cận ngang \(y={1 \over 2}\)

Bảng biến thiên:

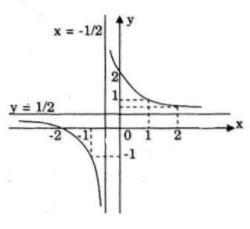
Đồ thị giao \(Ox\) tại điểm \((-2;0)\)

Đồ thị giao \(Oy\) tại điểm \((0;2)\)

LG b

Chứng minh rằng đường thẳng \(y = mx + m - 1\) luôn đi qua một điểm cố định của đường cong (H) khi m biến thiên.

Lời giải chi tiết:

Ta có \(y = mx + m - 1 \) \(\Leftrightarrow y + 1 = m\left( {x + 1} \right)\)

Tọa độ điểm cố định \(A\) của đường thẳng là nghiệm của hệ:

\(\left\{ \matrix{
x + 1 = 0 \hfill \cr 
y + 1 = 0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
x = - 1 \hfill \cr 
y = - 1 \hfill \cr} \right.\)

Vậy \(A(-1;-1)\)

Thay tọa độ của A vào công thức hàm số ta thấy: \( - 1 = \frac{{ - 1 + 2}}{{2.\left( { - 1} \right) + 1}}\) (đúng) nên \(A\) thuộc đường cong \((H)\).

Cách khác:

Gọi điểm cố định mà đường thẳng y = mx+m-1 luôn đi qua là I.

Ta có \(I\left( {{x_0};\frac{{{x_0} + 2}}{{2{x_0} + 1}}} \right) \in \left( H \right)\) thay vào phương trình y=mx+m-1 được:

Để phương trình (*) luôn đúng với mọi m khi và chỉ khi:

Vậy đường thẳng y=mx+m-1 luôn đi qua 1 điểm cố định I(-1; -1) của đường cong (H) khi m biến thiên.

LG c

Tìm các giá trị của m sao cho đường thẳng đã cho cắt đường cong \((H)\) tại hai điểm thuộc cùng một nhánh của (H).

Lời giải chi tiết:

Hoành độ giao điểm của đường thẳng đã cho và đường cong \((H)\) là nghiệm của phương trình:

\(\eqalign{
& m\left( {x + 1} \right) - 1 = {{x + 2} \over {2x + 1}}\cr & \Leftrightarrow \left( {2x + 1} \right)\left[ {m\left( {x + 1} \right) - 1} \right] = x + 2 \cr 
& \Leftrightarrow m\left( {x + 1} \right)\left( {2x + 1} \right) - \left( {2x + 1} \right) = x + 2 \cr 
&  \Leftrightarrow \left( {x + 1} \right)\left( {2mx + m} \right) - 3x - 3 = 0 \cr&\Leftrightarrow \left( {x + 1} \right)\left( {2mx + m} \right) - 3\left( {x + 1} \right) = 0\cr&\Leftrightarrow \left( {x + 1} \right)\left( {2mx + m - 3} \right) = 0\cr& \Leftrightarrow \left[ \matrix{
x = - 1 \hfill \cr 
f\left( x \right) = 2mx + m - 3 = 0\,\,\,\left( 1 \right) \hfill \cr} \right. \cr} \)

Hai nhánh của \((H)\) nằm về hai bên của tiệm cận đứng \(x =  - {1 \over 2}\)

Điểm \(A(-1;-1)\) thuộc nhánh trái của \((H)\) vì \({x_A} =  - 1 <  - {1 \over 2}\)

Đường thẳng cắt \((H)\) tại hai điểm thuộc cùng một nhánh khi và chỉ khi (1) có nghiệm \(x <  - {1 \over 2}\) và \(x \ne  - 1\) tức

\(\left\{ \matrix{
2m \ne 0 \hfill \cr 
x = {{ - m + 3} \over {2m}} < - {1 \over 2} \hfill \cr 
f\left( { - 1} \right) \ne 0 \hfill \cr} \right.\) \( \Leftrightarrow \left\{ \matrix{
m \ne 0 \hfill \cr 
- {1 \over 2}+{3 \over {2m}} < - {1 \over 2}  \hfill \cr 
- m - 3 \ne 0 \hfill \cr} \right. \)

\( \Leftrightarrow \left\{ \begin{array}{l}
m \ne 0\\
\frac{3}{{2m}} < 0\\
- m \ne 3
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
m \ne 0\\
m < 0\\
m \ne - 3
\end{array} \right.\)

\(\Leftrightarrow m < - 3\,\, \text{hoặc}\, - 3 < m < 0.\)

HocTot.Nam.Name.Vn