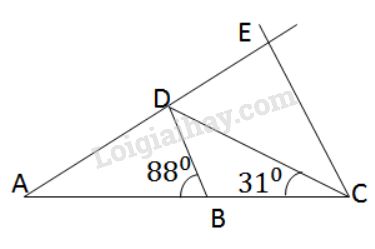
Bài 6 trang 92 SGK Toán 7 tập 2

Đề bài

Cho tam giác $ADC$ ($AD = DC$) có  $\widehat {ACD} = {31^o}$. Trên cạnh $AC$ lấy một điểm $B$ sao cho  $\widehat {ABD} = {88^o}$. Từ $C$ kẻ một tia song song với $BD$ cắt tia $AD$ ở $E.$

a) Hãy tính các góc $DCE$ và $DEC.$

b) Trong tam giác $CDE$, cạnh nào lớn nhất? Tại sao?  

Lời giải chi tiết

a) $∆ADC$ cân tại $D$ nên có  $\widehat {ACD} =\hat A = {31^o}$

$\Rightarrow \;  \widehat {ADC} = {180^o} - 2.  \widehat {ACD}$

$\Rightarrow$  $\widehat {ADC} = {180^o} - 2.{31^o} = {118^o}$

+ $∆ADB$ có  $\hat A = {31^o},\widehat {ABD} = {88^o}$

$\Rightarrow$  $\widehat {ADB} = {180^o} - \left( {{{31}^o} + {{88}^o}} \right)$ (định lí tổng ba góc trong tam giác )

Hay  $\widehat {ADB} = {61^o}$

+ Ta có $BD // CE$

$\Rightarrow$  $\widehat {DEC} = \widehat {ADB} = {61^o}$ (hai góc đồng vị)

+  $\widehat {EDC}$ là góc ngoài $∆ADC$ cân tại $D$

$\Rightarrow$  $\widehat {EDC} = 2.\hat C = {62^o}$

$∆DEC$ có  $\widehat {DEC} = {61^o};\widehat {EDC} = {62^o}$ 

Theo định lí tổng ba góc trong một tam giác ta có:

$\widehat {DCE} = {180^o} - (\widehat {DEC} + \widehat {EDC})$

           $= 180^o - (61^o + 62^o)= {57^0}$

b) Xét tam giác DEC có $\widehat {DCE} < \widehat {DEC} < \widehat {EDC}$ (do ${57^0} < {61^0} < {62^0})$ $\Rightarrow  DE < DC < CE$ (Theo định lí mối quan hệ giữa góc và cạnh đối diện trong tam giác).
Vậy $CE$ là cạnh lớn nhất.

HocTot.Nam.Name.Vn