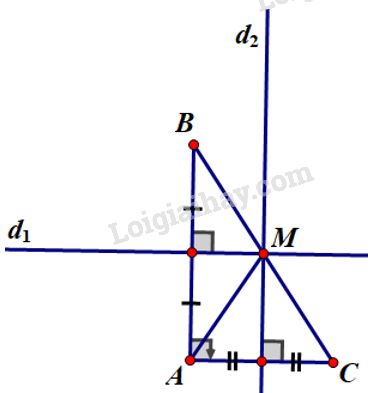
Bài 56 trang 80 SGK Toán 7 tập 2

Đề bài

Sử dụng bài $55$ để chứng minh rằng: Điểm cách đều ba đỉnh của một tam giác vuông là trung điểm của cạnh huyền của tam giác đó.

Từ đó hãy tính độ dài đường trung tuyến xuất phát từ đỉnh góc vuông theo độ dài cạnh huyền của một tam giác vuông.

Lời giải chi tiết

a) Giả sử $∆ABC$ vuông góc tại $A$. Vẽ hai đường thẳng $d_1,d_2$ lần lượt là các đường trung trực  của hai cạnh góc vuông $AB, AC$ cắt nhau tại $M.$ Ta chứng minh $M$ là trung điểm của $BC.$

Ta có $M$ là giao điểm hai đường trung trực ${d_1},{d_2}$ của $AB, AC$ (theo cách vẽ)

Theo kết quả của bài $55$ suy ra $B, M, C$ thẳng hàng.

Ta có:  $MA = MB$ (vì $M$ thuộc đường trung trực của $AB$)

           $MA = MC$ (vì $M$ thuộc đường trung trực của $AC$)

$\Rightarrow MB = MC=MA$

Do $B, M, C$ thẳng hàng và $M$ cách đều $B;C$ nên $M$ là trung điểm của $BC.$

b) $M$ là trung điểm $BC$  $\Rightarrow MB = \dfrac{1}{2} BC$.

Mà $AM = MB$ nên $MA =\dfrac{1}{2} BC$.

Vậy độ dài đường trung tuyến xuất phát từ đỉnh góc vuông của một tam giác vuông bằng một nửa độ dài cạnh huyền. 

HocTot.Nam.Name.Vn