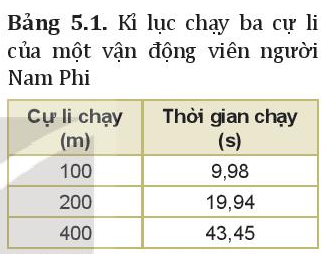
Bài 5. Tốc độ và vận tốc trang 26, 27, 28, 29 Vật Lí 10 Kết nối tri thứcMột vận động viên người Nam Phi đã lập kỉ lục thế giới về chạy ba cự li: 100 m, 200 m và 400 m (Bảng 5.1). Hãy dùng hai cách trên để xác định vận động viên này chạy nhanh nhất ở cự li nào. . Tại sao tốc độ này được gọi là tốc độ trung bình. . Hãy tính tốc độ trung bình ra m/s và km/h của nữ vận động viên tại một số giải thi đấu dựa vào Bảng 5.2. Bố bạn A đưa A đi học bằng xe máy vào lúc 7 giờ. Tính tốc độ trung bình của xe máy chở A khi đi từ nhà đến trường. Tính tốc độ của xe vào lúc 7 giờ 15 p Tổng hợp đề thi học kì 2 lớp 10 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa... Video hướng dẫn giải Câu hỏi tr 26 HĐ Video hướng dẫn giải
Phương pháp giải: - So sánh quãng đường đi được trong cùng một thời gian. - So sánh thời gian để đi cùng một quãng đường. Lời giải chi tiết: * Cách 1: So sánh quãng đường đi được trong cùng một thời gian. - Quãng đường vận động viên đi được trong 1 s ở mỗi cự li là: + Cự li 100 m: + Cự li 200 m: + Cự li 400 m: => Vận động viên chạy nhanh nhất trong cự li 200 m. * Cách 2: So sánh thời gian để đi cùng một quãng đường. - Thời gian để vận động viên chạy quãng đường 100 m ở mỗi cự li là: + Cự li 100 m: + Cự li 200 m: + Cự li 400 m: => Vận động viên chạy nhanh nhất ở cự li 200 m Câu hỏi tr 26 CH Video hướng dẫn giải
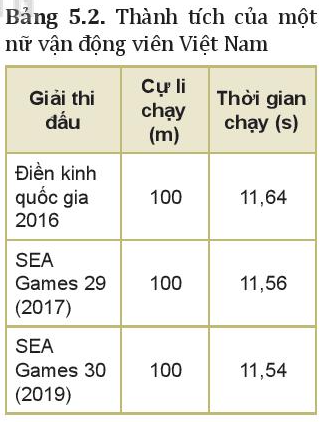
Phương pháp giải: 1. Sử dụng công thức tính tốc độ trung bình của chuyển động. 2. Sử dụng công thức tính tốc độ trung bình của chuyển động. Lời giải chi tiết: 1. Công thức 5.1b: Tốc độ này được gọi là tốc độ trung bình vì nó cho biết quãng đường vật đi được trong một thời gian xác định. 2. Tốc độ trung bình của nữ vận động viên tại các giải thi đấu là: - Điền kinh quốc gia 2016:
- SEA Games 29 (2017):
- SEA Games 29 (2019):
Câu hỏi tr 27 CH 1 Video hướng dẫn giải
Phương pháp giải: Sử dụng công thức tính tốc độ trung bình: Lời giải chi tiết: a) - Thời gian xe máy đi từ nhà đến trường là:
- Tốc độ trung bình của xe máy chở A khi đi từ nhà đến trường là:
b) Theo đề bài ta có: + Sau 5 phút kể từ khi xuất phát, xe đạt tốc độ 30 km/h + Sau 10 phút nữa, xe tăng tốc lên thêm 15 km/h Suy ra, tốc độ của xe vào lúc 7 giờ 15 phút là: + Xe dừng trước cổng trường lúc 7 giờ 30 phút => Tốc độ của xe lúc 7 giờ 30 phút là: => Tốc độ này là tốc độ tức thời. Câu hỏi tr 27 CH 2 Video hướng dẫn giải
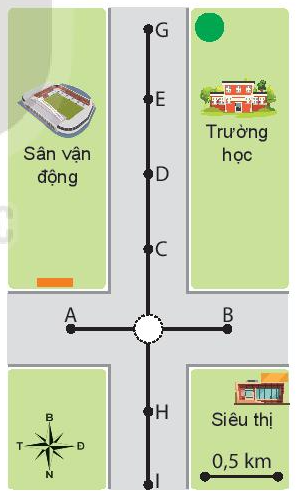
Phương pháp giải: Sử dụng công thức: Lời giải chi tiết: Đổi: 3 phút = 0,05 giờ Quãng đường người đó đi được sau 3 phút là: Ta có: Vậy sau 3 phút, người đó đến vị trí E trên hình. Câu hỏi tr 27 CH 3 Video hướng dẫn giải
Lời giải chi tiết: Biểu thức xác định giá trị vận tốc là biểu thức : c) Vì d là độ dịch chuyển của vật sẽ cho chúng ta biết được độ dịch chuyển của vật trong một đơn vị thời gian xác định. Câu hỏi tr 28 CH 1 Video hướng dẫn giải
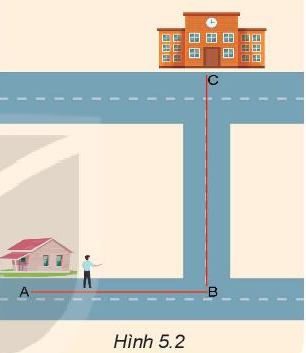
Phương pháp giải: - Xác định độ dài quãng đường từ nhà đến trường - Xác định thời gian từ nhà đến trường - Xác định độ dịch chuyển từ nhà đến trường - Sử dụng công thức tính tốc độ trung bình và vận tốc trung bình. Lời giải chi tiết: - Độ dài quãng đường từ nhà đến trường là:
- Thời gian đi từ nhà đến trường là: (phút) - Tốc độ trung bình của bạn A khi đi từ nhà đến trường là:
- Độ dịch chuyển của bạn A là:
- Vận tốc trung bình của bạn A khi đi từ nhà đến trường là:
Câu hỏi tr 28 CH 2 Video hướng dẫn giải
Phương pháp giải: Sử dụng công thức tổng hợp vận tốc. Lời giải chi tiết: 1. Đổi: 36 km/h = 10 m/s Gọi: là vận tốc của hành khách so với tàu là vận tốc của tàu so với mặt đường là vận tốc của hành khách so với mặt đường Suy ra, ta có: Do hành khách chuyển động về cuối đoàn tàu, tức là ngược chiều chuyển động của đoàn tàu nên ta có:
Vậy vận tốc của hành khách đối với mặt đường trong trường hợp này là 9 m/s. 2. Gọi: là vận tốc của người so với nước là vận tốc của nước so với bờ là vận tốc của người so với bờ Ta có: - Khi người bơi trong bể nước yên lặng, tức , ta có:
- Khi người này bơi xuôi dòng chảy với vận tốc , ta có:
Vậy nếu người này bơi xuôi dòng sông có dòng chảy với vận tốc 1 m/s thì có thể đạt vận tốc tối đa là 2 m/s. 3. Gọi: là vận tốc của canô so với nước là vận tốc của nước so với bờ là vận tốc của canô so với bờ Ta có: - Khi canô chạy trên mặt nước yên lặng, tức , ta có:
- Khi canô chạy xuôi dòng sông, ta có:
(1) - Khi canô quay lại, ta có:
(2) - Từ (1) và (2) ta suy ra: Vậy vận tốc chảy của dòng sông là 7,17 km/h. Câu hỏi tr 29 Video hướng dẫn giải
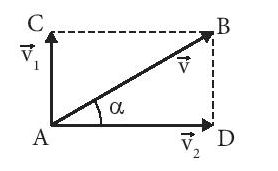
Phương pháp giải: - Sử dụng lý thuyết tổng hợp hai vận tốc vuông góc với nhau. - Sử dụng công thức tính tốc độ trung bình. Lời giải chi tiết: 1. Gọi: là vận tốc của máy bay so với gió là vận tốc của gió so với đường bay là vận tốc của máy bay so với đường bay Suy ra: Vận tốc tổng hợp của máy bay lúc này là:
2.
Vận tốc tổng hợp của máy bay: Vì nên và đều là một nửa của tam giác đều nên và AD là phương nằm ngang theo hướng Đông.
>> Học trực tuyến Lớp 10 cùng thầy cô giáo giỏi tại Tuyensinh247.com, (Xem ngay) Cam kết giúp học sinh học tốt, bứt phá điểm 9,10 chỉ sau 3 tháng, làm quen kiến thức, định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 10
|