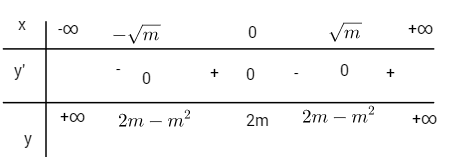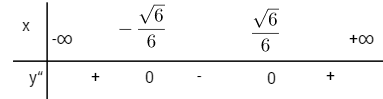Bài 48 trang 45 SGK giải tích 12 nâng cao

LG a

Tìm các giá trị của \(m\) sao cho hàm số có ba cực trị.

Lời giải chi tiết:

TXĐ: \(D =\mathbb R\)

\(y = 4{x^3} - 4mx = 4x\left( {{x^2} - m} \right)\)

\(y' = 0 \Leftrightarrow \left[ \matrix{
x = 0 \hfill \cr 
{x^2} = m \hfill \cr} \right.\)

Nếu \(m> 0\) thì \(y’=0\) \( \Leftrightarrow x = 0\) hoặc \(x =  - \sqrt m \) hoặc \(x = \sqrt m \)

Hàm số có ba điểm cực trị.
Nếu \(m \le 0\) thì \({x^2} - m \ge 0\) với mọi \(x \in\mathbb R\)

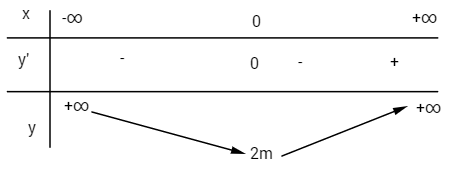
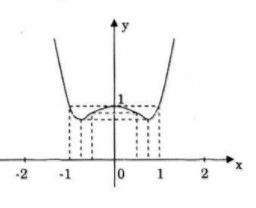
Hàm số có \(1\) cực tiểu.
Vậy hàm số có ba cực trị khi và chỉ khi \(m>0\).

Chú ý:

Có thể trình bày ngắn gọn như sau:

Để hàm số đã cho có 3 cực trị thì phương trình y’=0 có 3 nghiệm phân biệt

\( \Leftrightarrow \left\{ \begin{array}{l}m \ne 0\\m > 0\end{array} \right. \Leftrightarrow m > 0\)

Vậy với m > 0 thì hàm số đã cho có 3 điểm cực trị.

LG b

Kháo sát sự biến thiên và vẽ đồ thị của hàm số với \(m = {1 \over 2}\). Viết phương trình tiếp tuyến của đồ thị tại hai điểm uốn.

Lời giải chi tiết:

Với \(m = {1 \over 2}\) ta có \(y = {x^4} - {x^2} + 1\)
TXĐ: \(D =\mathbb R\)

\(\eqalign{
& \mathop {\lim }\limits_{x \to \pm \infty } y = + \infty \cr 
& y' = 4{x^3} - 2x = 2x\left( {2{x^2} - 1} \right)\cr&y' = 0 \Leftrightarrow \left[ \matrix{
x = 0 \hfill \cr 
x = \pm \sqrt {{1 \over 2}}  \hfill \cr} \right. \cr} \)

\(y\left( 0 \right) = 1\) và \(y\left( { \pm \sqrt {{1 \over 2}} } \right) = {3 \over 4}\)

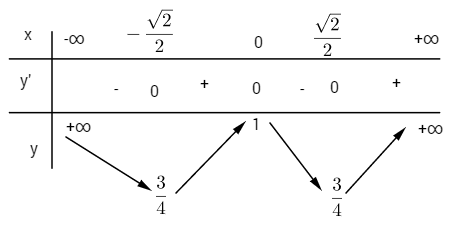
Hàm số đồng biến trên các khoảng \(\left( { - \frac{{\sqrt 2 }}{2};0} \right)\) và \(\left( {\frac{{\sqrt 2 }}{2}; + \infty } \right)\)

Hàm số nghịch biến trên các khoảng \(\left( { - \infty ; - \frac{{\sqrt 2 }}{2}} \right)\) và \(\left( {0;\frac{{\sqrt 2 }}{2}} \right)\)

Hàm số đạt cực đại tại \(x = 0\) và \({y_{CD}} = 1\)

Hàm số đạt cực tiểu tại \(x =  \pm \frac{{\sqrt 2 }}{2}\) và \({y_{CT}} =   \frac{3}{4}\)

\(y'' = 12{x^2} - 2\)

\(y'' = 0 \Leftrightarrow x =  \pm {{\sqrt 6 } \over 6};\,\,y\left( { \pm {{\sqrt 6 } \over 6}} \right) = {{31} \over {36}}\)

Xét dấu y”

Đồ thị có hai điểm uốn: \({I_1}\left( { - {{\sqrt 6 } \over 6};{{31} \over {36}}} \right)\) và \({I_2}\left( {{{\sqrt 6 } \over 6};{{31} \over {36}}} \right)\)
Điểm đặc biệt: \(x =  \pm 1 \Rightarrow y = 1\)

Đồ thị: Đồ thị nhận trục tung làm trục đối xứng.

Ta có: \(y'\left( { - \frac{{\sqrt 6 }}{6}} \right) = 4.{\left( { - \frac{{\sqrt 6 }}{6}} \right)^3} - 2.\left( { - \frac{{\sqrt 6 }}{6}} \right) \) \(= \frac{4}{{3\sqrt 6 }}\)

Do đó phương trình tiếp tuyến tại \({I_1}\left( { - {{\sqrt 6 } \over 6};{{31} \over {36}}} \right)\) là \(y - {{31} \over {36}} = y'\left( { - {{\sqrt 6 } \over 6}} \right)\left( {x + {{\sqrt 6 } \over 6}} \right)\)

\( \Leftrightarrow y = {4 \over {3\sqrt 6 }}x + {{13} \over {12}}\)

Lại có \(y'\left( { \frac{{\sqrt 6 }}{6}} \right) = 4.{\left( {  \frac{{\sqrt 6 }}{6}} \right)^3} - 2.\left( {  \frac{{\sqrt 6 }}{6}} \right) \) \(= -\frac{4}{{3\sqrt 6 }}\)

Do đó phương trình tiếp tuyến tại \({I_2}\left( {{{\sqrt 6 } \over 6};{{31} \over {36}}} \right)\) là: \(y - {{31} \over {36}} = y'\left( {  {{\sqrt 6 } \over 6}} \right)\left( {x - {{\sqrt 6 } \over 6}} \right)\) \(\Leftrightarrow y =  - {4 \over {3\sqrt 6 }}x + {{13} \over {12}}\)

HocTot.Nam.Name.Vn