Bài 41 trang 73 SGK Toán 7 tập 2

Đề bài

Hỏi trọng tâm của một tam giác đều có cách đều ba cạnh của nó hay không? Vì sao?

Lời giải chi tiết

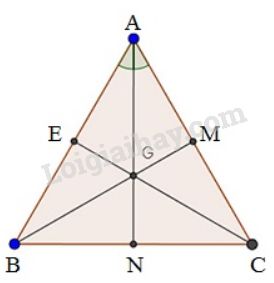
Cách 1: 

Giả sử $∆ABC$ đều, 3 đường trung tuyến AN, BM và CE cắt nhau tại G nên G là trọng tâm của $∆ABC$ 

Vì $∆ABC$ đều nên 3 đường trung tuyến đồng thời là 3 đường phân giác 

$\Rightarrow$ G là giao điểm của 3 đường phân giác của $∆ABC$

$\Rightarrow$ $G$ cách đều ba cạnh của tam giác $ABC$ ( Tính chất 3 đường phân giác của tam giác)

Cách 2:

Giả sử $∆ABC$ đều có trọng tâm $G$. Các điểm $E, N, M$ lần lượt là trung điểm của $AB, BC, AC.$

$\Rightarrow GA = \dfrac{2}{3}AN$;  $GB = \dfrac{2}{3}BM$;  $GC = \dfrac{2}{3}EC$.

Vì $∆ABC$ đều nên ba trung tuyến $AN, BM, CE$ bằng nhau (áp dụng chứng minh bài 29 trang 67 SGK toán 7 tập 2)

$\Rightarrow GA = GB = GC$

Xét $∆AMG$ và $∆CMG$ ta có:

+) $GA = GC$ (chứng minh trên)

+) $AM = MC$ (vì $M$ là trung điểm của $AC$)

+) Cạnh $MG$ chung

Vậy $∆AMG = ∆CMG$ (c.c.c)

$\Rightarrow$ $\widehat{AMG}=\widehat{CMG}$

Mà $\widehat{AMG}+\widehat{CMG} = 180^o$ ($2$ góc kề bù)

$\Rightarrow$ $\widehat{AMG} = 90^o$ 

$\Rightarrow GM ⊥ AC$ tức là $GM$ là khoảng cách từ $G$ đến $AC$.

Chứng minh tương tự $GE, GN$ là khoảng cách từ $G$ đến $AB, BC.$

Mà $GM =\dfrac{1}{3}BM$; $GN = \dfrac{1}{3}AN$; $GE = \dfrac{1}{3}EC$.

Và $AN = BM = EC$ nên $GM = GN = GE.$

Hay $G$ cách đều ba cạnh của tam giác $ABC.$