Bài 40 trang 43 Giải tích 12 Nâng cao

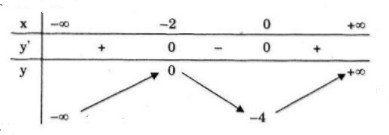
LG a

Khảo sát sự biến thiên và vẽ đồ thị của hàm số \(y = {x^3} + 3{x^2} - 4\)

Lời giải chi tiết:

Tập xác đinh: \(D=\mathbb R\)

Sự biến thiên:

\(\eqalign{
& y' = 3{x^2} + 6x \cr 
& y' = 0 \Leftrightarrow \left[ \matrix{
x = 0 \hfill \cr 
x = - 2 \hfill \cr} \right. \cr} \)

- Hàm số đồng biến trên khoảng \(\left( { - \infty ; - 2} \right)\) và \(\left( {0; + \infty } \right)\)

- Hàm số nghịch biến trên khoảng \((-2;0)\)

- Cực trị:

  Hàm số đạt cực đại tại \(x=-2\;;y_{CĐ}=0\)

  Hàm số đạt cực tiểu tại \(x=0\;;y_{CT}=-4\)

- Giới hạn:

\(\eqalign{
& \mathop {\lim }\limits_{x \to + \infty } \left( {{x^3} + 3{x^2} - 4} \right) = + \infty \cr 
& \mathop {\lim }\limits_{x \to - \infty } \left( {{x^3} + 3{x^2} - 4} \right) = - \infty \cr} \)

\(\eqalign{
& y'' = 6x + 6 \cr 
& y'' = 0 \Leftrightarrow x = - 1 \cr} \)

Điểm uốn \(I(-1;-2)\)

- Bảng biến thiên:

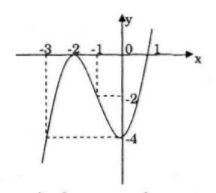
Đồ thị:

Đồ thị hàm số nhận điiểm \(I(-1;-2)\) làm tâm đối xứng.

LG b

Viết phương trình tiếp tuyến của đồ thị tại điểm uốn.

Phương pháp giải:

Công thức viết phương trình tiếp tuyến của ĐTHS tại điểm \({M_0}\left( {{x_0};f\left( {{x_0}} \right)} \right)\) là:

\(y - f\left( {{x_0}} \right) = f'\left( {{x_0}} \right)\left( {x - {x_0}} \right)\) hay \(y = f'\left( {{x_0}} \right)\left( {x - {x_0}} \right) + f\left( {{x_0}} \right)\)

Lời giải chi tiết:

\(y'(-1)=3.(-1)^2+6.(-1)=-3\)

Phương trình tiếp tuyến với đồ thị tại \(I(-1;-2)\) là:

\(y=-3(x+1)+(-2) \) \(\Leftrightarrow y =  - 3x - 5\)

LG c

Chứng minh rằng điểm uốn là tâm đối xứng của đồ thị.

Lời giải chi tiết:

Cách 1. Gọi I(-1; -2) là tọa độ điểm uốn.

Theo công thức đổi trục tọa độ theo véc tơ OI ta có: \(\left\{ \begin{array}{l}x = X - 1\\y = Y - 2\end{array} \right.\)

Phương trình của \(\left( C \right)\) trong hệ tọa độ \(IXY\) là:

\(\begin{array}{l}Y - 2 = {\left( {X - 1} \right)^3} + 3{\left( {X - 1} \right)^2} - 4\\ \Leftrightarrow Y - 2 = {X^3} - 3{X^2} + 3X + 1 + 3{X^2} - 6X + 3 - 4\\ \Leftrightarrow Y = {X^3} - 3X\end{array}\)

Hàm số \(Y = {X^3} - 3X\) là hàm số lẻ nên đồ thị nhận điểm uốn làm tâm đối xứng

⇒ điều phải chứng minh

Cách 2:

Lấy điểm \({M_1}\left( {{x_1};{y_1}} \right)\) bất kì thuộc \(\left( C \right)\).

Điểm \({M_2}\left( {{x_2};{y_2}} \right)\) đối xứng với \({M_1}\) qua \(I\left( { - 1; - 2} \right)\)

\( \Leftrightarrow \left\{ \begin{array}{l} - 1 = \frac{{{x_1} + {x_2}}}{2}\\ - 2 = \frac{{{y_1} + {y_2}}}{2}\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}{x_2} =  - 2 - {x_1}\\{y_2} =  - 4 - {y_1}\end{array} \right.\) \( \Rightarrow {M_2}\left( { - 2 - {x_1}; - 4 - {y_1}} \right)\)

Ta kiểm tra \(M_2\) có thuộc đồ thị hàm số đã cho hay không. Ta có:

\(\begin{array}{l}{\left( { - 2 - {x_1}} \right)^3} + 3{\left( { - 2 - {x_1}} \right)^2} - 4\\ =  - 8 - 12{x_1} - 6x_1^2 - x_1^3 + 3\left( {4 + 4{x_1} + x_1^2} \right) - 4\\ =  - 8 - 12{x_1} - 6x_1^2 - x_1^3 + 12 + 12{x_1} + 3x_1^2 - 4\\ =  - 3x_1^2 - x_1^3 = 4 - \left( {x_1^3 + 3x_1^2 - 4} \right)\\ = 4 - {y_1}\end{array}\)

Do đó điểm \({M_2}\left( { - 2 - {x_1}; - 4 - {y_1}} \right)\) cũng thuộc \(\left( C \right)\).

Vậy \(I\left( { - 1; - 2} \right)\) là tâm đối xứng của \(\left( C \right)\).

Cách 3:

Sử dụng lý thuyết: Đồ thị hàm số y=f(x) nhận \(I\left( {{x_0};{y_0}} \right)\) làm tâm đối xứng

\( \Leftrightarrow \) f(x₀+x)+f(x₀-x)=2y₀ với ∀x

Áp dụng:

Đồ thị nhận I(-1; -2) là tâm đối xứng khi và chỉ khi:

⇔ f(-1+x)+f(-1-x)=-4 với ∀x

\(\eqalign{
& \Leftrightarrow {\left( { - 1 + x} \right)^3} + 3{\left( { - 1 + x} \right)^2} - 4 \cr&+ {\left( { - 1 - x} \right)^3} + 3{\left( { - 1 - x} \right)^2} - 4 = - 4 \cr 
& \Leftrightarrow - 1 + 3x - 3{x^2} + {x^3} + 3 - 6x + 3{x^2} - 4 \cr&- 1 - 3x - 3{x^2} - {x^3} + 3 + 6x + 3{x^2} - 4 = - 4 \cr 
& \Leftrightarrow - 4 = - 4\,\,\forall x \cr} \)

\(\Leftrightarrow I(-1;-2)\) là tâm đối xứng của đồ thị.

HocTot.Nam.Name.Vn