Bài 4 trang 70 SGK Hình học 10 nâng caoTrên hình 63 có vẽ hai tam giác vuông cân ABC và A'B'C' có chung đỉnh A. GÓP Ý HAY - NHẬN NGAY QUÀ CHẤT Gửi góp ý cho HocTot.Nam.Name.Vn và nhận về những phần quà hấp dẫn
Lựa chọn câu để xem lời giải nhanh hơn
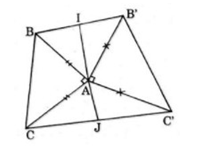
Trên hình 63 có vẽ hai tam giác vuông cân ABC và AB'C' có chung đỉnh A. Gọi I và J lần lượt là trung điểm của hai đoạn thẳng BB' và CC'.
Chứng minh rằng LG a AI⊥CC′,AJ⊥BB′ Phương pháp giải: Để chứng minh các đường thẳng vuông góc, ta thực hiện nhân vô hướng các véc tơ và kiểm tra tích đó bằng 0. Lời giải chi tiết: Vì I là trung điểm BB' và J là trung điểm CC' nên: →AI=12(→AB+→AB′) →AJ=12(→AC+→AC′) ⇒→AI.→CC′=12(→AB+→AB′).(→AC′−→AC)=12(→AB.→AC′−→AB.→AC+→AB′.→AC′−→AB′.→AC) Vì AB⊥AC,AB′⊥AC′ nên →AB.→AC=→AB′.→AC′=0 ⇒→AI.→CC′=12(→AB.→AC′−→AB′.→AC) Mặt khác →AB.→AC′=AB.AC′.cos^BAC′→AB′.→AC=AB′.AC.cos^B′AC Do ABC, AB’C’ vuông cân tại A nên AC’=AC,AB’=AB Lại có: ^BAC′=^BAB′+^B′AC′=^BAB′+900^B′AC=^B′AB+^BAC=^B′AB+900⇒^BAC′=^B′AC⇒cos^BAC′=cos^B′AC Do đó, →AB.→AC′=→AB′.→AC ⇒→AB.→AC′−→AB′.→AC=0 ⇒→AI.→CC′=0⇔AI⊥CC′ Tương tự →AJ.→BB′ =12(→AC+→AC′).(→AB′−→AB) =12(→AC.→AB′−→AC.→AB+→AC′.→AB′−→AC′.→AB)=12(→AC.→AB′−→AC′.→AB)=0⇒AJ⊥BB′ LG b BC′⊥B′C Lời giải chi tiết: Ta có →BC′.→B′C=(→AC′−→AB).(→AC−→AB′)=→AC′.→AC−→AC′.→AB′−→AB.→AC+→AB.→AB′ =→AC′.→AC+→AB.→AB′ (vì →AB.→AC=→AB′.→AC′=0) →AB.→AB′=AB.AB′.cos^BAB′ →AC.→AC′=AC.AC′.cos(1800−^BAB′) =−→AB.→AB′. Do đó: →AC′.→AC+→AB.→AB′=−→AB.→AB′+→AB.→AB′=0 Suy ra →BC′.→B′C=→0 Vậy BC′⊥B′C. HocTot.Nam.Name.Vn  Chia sẻ Bình luận
PH/HS Tham Gia Nhóm Lớp 10 Để Trao Đổi Tài Liệu, Học Tập Miễn Phí!
|
