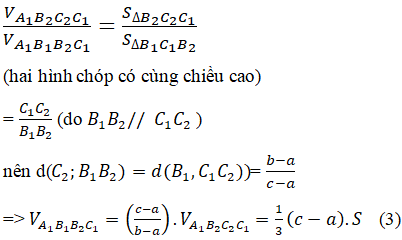Bài 4 trang 31 SGK Hình học 12 Nâng caoCho khối làng trụ đứng ABC.A’B'C’ có diện tích đáy bằng S và AA' = h. Một mặt phẳng (P) cắt các cạnh AA', BB’, CC'
Lựa chọn câu để xem lời giải nhanh hơn
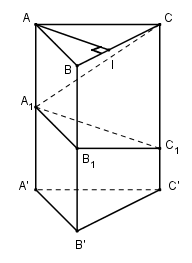
Cho khối lăng trụ đứng \(ABC.A’B'C’\) có diện tích đáy bằng \(S\) và \(AA' = h\). Một mặt phẳng \((P)\) cắt các cạnh \(AA', BB’, CC'\) lần lượt tại \({A_1},{B_1}\) và \(C_1\). Biết \(A{A_1} = a,B{B_1} = b,CC_1 = c\). LG a Tính thể tích hai phần của khối lăng trụ được phân chia bởi mặt phẳng \((P)\). Lời giải chi tiết:
Kẻ đường cao \(AI\) của tam giác \(ABC\) thì \(AI \bot \left( {BCC'B'} \right)\) \(\Rightarrow AI = d\left( {{A_1};\left( {BCC'B'} \right)} \right)\). Ta có: \(\eqalign{ Cách khác:
Không làm mất tính tổng quát, giả sử a≤b≤c. Trên cạnh BB’ lấy B2 sao cho BB2=a B1B2=b-a Trên cạnh CC’ lấy C2 sao cho CC2=a C1C2=c-a Ta có: \({V_{ABC.{A_1}{B_1}{C_1}}} \) \(= {V_{ABC.{A_1}{B_2}{C_2}}} + {V_{{A_1}{B_2}{C_2}{B_1}}} + {V_{{A_1}{B_1}{C_2}{C_1}}}\) Trong đó: \(\begin{array}{l}{V_{ABC.{A_1}{B_2}{C_2}}} = A{A_1}.{S_{ABC}} = aS\left( 1 \right)\\{V_{{A_1}{B_2}{C_2}{B_1}}} = \frac{1}{3}{B_1}{B_2}.{S_{{A_1}{B_2}{C_2}}}\\ = \frac{1}{3}\left( {b - a} \right)S\left( 2 \right)\end{array}\) (vì B1 B2⊥(A1 B2 C2 ); ∆A1 B2 C2=∆ABC)
Thay (1), (2) và (3) vào (*) ta được:
LG b Với điều kiện nào của \(a, b, c\) thì thể tích hai phần đó bằng nhau ? Lời giải chi tiết: \({V_{ABC.{A_1}{B_1}{C_1}}} = {V_{{A_1}{B_1}{C_1}.A'B'C'}} \) \(\Leftrightarrow {1 \over 3}\left( {a + b + c} \right)S = \frac{1}{3}S\left( {3h - a - b - c} \right) \) \( \Leftrightarrow a + b + c = 3h - a - b - c\) \(\Leftrightarrow 3h = 2\left( {a + b + c} \right)\) HocTot.Nam.Name.Vn
|