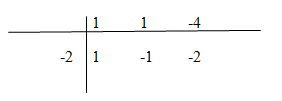Bài 39 trang 36 SGK giải tích 12 nâng cao

LG a

\(y = {{{x^2} + x - 4} \over {x + 2}}\)

Lời giải chi tiết:

\(y = x - 1 - {2 \over {x + 2}}\)

TXĐ: \(D =\mathbb R\backslash \left\{ { - 2} \right\}\)

+) Tìm các đường tiệm cận:

\(\mathop {\lim }\limits_{x \to {{\left( { - 2} \right)}^ + }} y =  - \infty \) và \(\mathop {\lim }\limits_{x \to {{\left( { - 2} \right)}^ - }} y =  + \infty \) nên \(x = -2\) là tiệm cận đứng.
\(\mathop {\lim }\limits_{x \to  \pm \infty } \left[ {y - \left( {x - 1} \right)} \right] = \mathop {\lim }\limits_{x \to  \pm \infty } {{ - 2} \over {x + 2}}=0\) nên \(y = x -1\) là tiệm cận xiên.

Chú ý:

Áp dụng cách chia như bài 38 để viết lại hàm số theo lược đồ dưới đây:

+) Tìm giao điểm hai đường tiệm cận:

Gọi I là giao điểm hai đường tiệm cận, tọa độ của I thỏa mãn hệ phương trình 

\(\left\{ \begin{array}{l}
x = - 2\\
y = x - 1
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
x = - 2\\
y = - 3
\end{array} \right. \) \(\Rightarrow I\left( { - 2; - 3} \right)\)

+ Công thức chuyển hệ tọa độ trong phép tịnh tiến theo vectơ OI là: \(\left\{ \begin{array}{l}x = X - 2\\y = Y - 3\end{array} \right.\)

+) Phương trình của đường cong (C1) trong hệ tọa độ IXY:

\(\begin{array}{l}y = x - 1 - \frac{2}{{x + 2}}\\ \Leftrightarrow Y - 3 = X - 2 - 1 - \frac{2}{{X - 2 + 2}}\\ \Leftrightarrow Y = X - \frac{2}{X}\end{array}\)

Vậy (C1) trong hệ tọa độ IXY có phương trình \(Y = X - \frac{2}{X}\)

Đây là hàm số lẻ nên đồ thị (C₁) nhận gốc tọa độ I làm tâm đối xứng.

LG b

\(y = {{{x^2} - 8x + 19} \over {x - 5}}\)

Lời giải chi tiết:

 Ta có: \(y = x - 3 + \frac{4}{{x - 5}}\) \(\left( {{C_2}} \right)\)

+ Tiệm cận xiên của đồ thị (C₂) là đường thẳng y=x-3

(Vì \(\mathop {\lim }\limits_{x \to  \pm \infty } \left[ {y - \left( {x - 3} \right)} \right]\)\( = \mathop {\lim }\limits_{x \to  \pm \infty } \left( {x - 3 + \frac{4}{{x - 5}} - x + 3} \right)\)  \( = \mathop {\lim }\limits_{x \to  \pm \infty } \left( {\frac{4}{{x - 5}}} \right) = 0\))

Tiệm cận đứng của đồ thị là đường thẳng x = 5

(vì \(\mathop {\lim }\limits_{x \to {5^ + }} y = \mathop {\lim }\limits_{x \to {5^ + }} \left( {x - 3 + \frac{4}{{x - 5}}} \right) =  + \infty \) và \(\mathop {\lim }\limits_{x \to {5^ - }} y = \mathop {\lim }\limits_{x \to {5^ - }} \left( {x - 3 + \frac{4}{{x - 5}}} \right) =  - \infty \))

+ Giao điểm I của hai tiệm cận có tọa độ thỏa mãn hệ phương trình \(\left\{ \begin{array}{l}x = 5\\y = x - 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 5\\y = 2\end{array} \right.\)

Vậy I(5; 2)

+ Công thức chuyển hệ tọa độ trong phép tịnh tiến theo véc tơ OI là \(\left\{ \begin{array}{l}x = X + 5\\y = Y + 2\end{array} \right.\)

+ Phương trình của đường cong (C₂) trong hệ tọa độ IXY:

Ta có:

\(\begin{array}{l}y = x - 3 + \frac{4}{{x - 5}}\\ \Leftrightarrow Y + 2 = X + 5 - 3 + \frac{4}{{X + 5 - 5}}\\ \Leftrightarrow Y = X + \frac{4}{X}\end{array}\)

Đây là hàm lẻ nên đồ thị (C₂) nhận gốc tọa độ I làm tâm đối xứng.

HocTot.Nam.Name.Vn