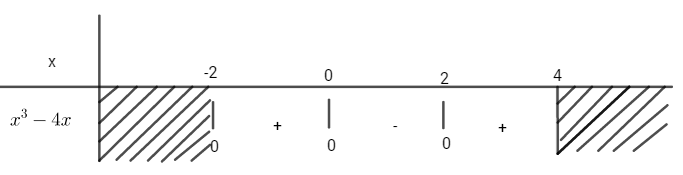Bài 28 Trang 167 SGK Đại số và Giải tích 12 Nâng caoTính diện tích hình phẳng giới hạn bởi:
Lựa chọn câu để xem lời giải nhanh hơn
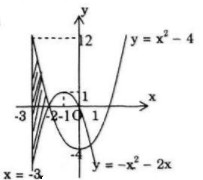
Tính diện tích hình phẳng giới hạn bởi: LG a Đồ thị các hàm số y=x2−4, y=−x2−2x và đường thẳng x=−3,x=−2; Phương pháp giải: Tính diện tích hình phẳng giới hạn bởi các đồ thị hàm số y=f(x),y=g(x), x=a,x=b. +) B1: Tìm nghiệm a≤x1<x2<...<xn≤b của phương trình hoành độ giao điểm f(x)=g(x). +) B2: Tính diện tích theo công thức: S=b∫a|f(x)−g(x)|dx =x1∫a|f(x)−g(x)|dx +x2∫x1|f(x)−g(x)|dx +...+xn∫xn−1|f(x)−g(x)|dx +b∫xn|f(x)−g(x)|dx =|x1∫a[f(x)−g(x)]dx|+|x2∫x1[f(x)−g(x)]dx| +...+|xn∫xn−1[f(x)−g(x)]dx| +|b∫xn[f(x)−g(x)]dx| Lời giải chi tiết: Cách 1: Tính diện tích theo công thức Ta có: x2−4=−x2−2x ⇔2x2+2x−4=0 ⇔[x=1x=−2 Có −3<−2<1 nên S=−2∫−3|x2−4−(−x2−2x)|dx =−2∫−3|2x2+2x−4|dx =|−2∫−3(2x2+2x−4)dx| =|(2.x33+2.x22−4x)−2−3| =|203−3|=113 Cách 2: Xét dấu Ta có
Ta thấy, khi −3≤x≤−2 thì 2x2+2x−4≥0 ⇒|2x2+2x−4|=2x2+2x−4. Do đó, S=−2∫−3|x2−4−(−x2−2x)|dx =−2∫−3(2x2+2x−4)dx =2−2∫−3(x2+x−2)dx =2(x33+x22−2x)|−2−3=113 Chú ý: Khi việc xét dấu phức tạp ta nên làm theo cách 1 sẽ tránh được việc lập bảng xét dấu. LG b Đồ thị hai hàm số y=x2 và y=−x2−2x Lời giải chi tiết: Cách 1: Phương trình hoành độ giao điểm của hai đồ thị là: x2−4=−x2−2x⇔x2+x−2=0 ⇔[x=−2x=1 S=1∫−2|x2−4−(−x2−2x)|dx =1∫−2|2x2+2x−4|dx =|1∫−2(2x2+2x−4)dx| =|(2x33+2x22−4x)1−2| =|−73−203|=|−9|=9 Cách 2: Phương trình hoành độ giao điểm của hai đồ thị là: x2−4=−x2−2x⇔x2+x−2=0 ⇔[x=−2x=1 Ta thấy, khi −2≤x≤1 thì 2x2+2x−4≤0 ⇒|2x2+2x−4|=−2x2−2x+4. Do đó, S=1∫−2|x2−4−(−x2−2x)|dx =1∫−2|2x2+2x−4|dx =1∫−2(−2x2−2x+4)dx =(−2x33−x2+4x)|1−2=9 LG c Đồ thị hàm số y=x3−4x, trục hoành, đường thẳng x=-2 và đường thẳng x=4 Lời giải chi tiết: Cách 1: Ta có: x3−4x=0⇔x(x2−4)=0 ⇔[x=0x=2x=−2 Ta thấy, −2<0<2<4 ⇒S=4∫−2|x3−4x|dx =0∫−2|x3−4x|dx+2∫0|x3−4x|dx +4∫2|x3−4x|dx =|0∫−2(x3−4x)dx|+|2∫0(x3−4x)dx| +|4∫2(x3−4x)dx| =|(x44−4x22)0−2|+|(x44−4x22)20| +|(x44−4x22)42| =|0−(−4)|+|−4−0|+|32−(−4)| =44 Cách 2:
S=4∫−2|x3−4x|dx =0∫−2(x3−4x)dx−2∫0(x3−4x)dx +4∫2(x3−4x)dx =(x44−4x22)0−2−(x44−4x22)20 +(x44−4x22)42 =4−(−4)+36 =44 HocTot.Nam.Name.Vn
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM; 70+ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, 3 bước chi tiết: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng đáp ứng mọi kì thi.
|