Bài 22 trang 90 SGK Hình học 12 Nâng cao

LG a

Tam giác ABC có ba góc nhọn.

Phương pháp giải:

Sử dụng tính chất: Góc có cô sin dương thì là góc nhọn.

Lời giải chi tiết:

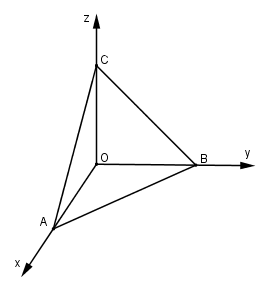
Chọn hệ trục tọa độ Oxyz như hình vẽ.
Ta có \(A\left( {a;0;0} \right)\,,\,B\left( {0;b;0} \right)\,,\,C\left( {0;0;c} \right)\) \(\left( {a > 0,b > 0,c > 0} \right)\)
Ta có \(\overrightarrow {AB}  = \left( { - a;b;0} \right);\overrightarrow {AC}  = \left( { - a;0;c} \right) \) \(\Rightarrow \overrightarrow {AB} .\overrightarrow {AC}  = {a^2} > 0 \) \(\Rightarrow \cos A = {{\overrightarrow {AB} .\overrightarrow {AC} } \over {AB.AC}} > 0\)

\( \Rightarrow \) A là góc nhọn.

Tương tự các góc B, C của tam giác ABC cũng nhọn.

LG b

\({\cos ^2}\alpha  + co{s^2}\beta  + {\cos ^2}\gamma  = 1\)

Lời giải chi tiết:

Mp(ABC) có phương trình \({x \over a} + {y \over b} + {z \over c} = 1\) nên có vectơ pháp tuyến \(\overrightarrow n  = \left( {{1 \over a};{1 \over b};{1 \over c}} \right)\).
Mp(OBC) \( \equiv \) Mp(Oyz) có vectơ pháp tuyến \(\overrightarrow i  = \left( {1;0;0} \right)\).
Gọi \(\alpha \) là góc giữa mp(ABC) và mp(OBC) thì:

\({\cos ^2}\alpha  = {\left( {{{\left| {\overrightarrow n .\overrightarrow i } \right|} \over {\left| {\overrightarrow n } \right|\left| {\overrightarrow i } \right|}}} \right)^2} = {{{1 \over {{a^2}}}} \over {{1 \over {{a^2}}} + {1 \over {{b^2}}} + {1 \over {{c^2}}}}}\)

Tương tự \({\cos ^2}\beta  = {{{1 \over {{b^2}}}} \over {{1 \over {{a^2}}} + {1 \over {{b^2}}} + {1 \over {{c^2}}}}}\) và \({\cos ^2}\gamma  = {{{1 \over {{c^2}}}} \over {{1 \over {{a^2}}} + {1 \over {{b^2}}} + {1 \over {{c^2}}}}}\)

Từ đó suy ra \({\cos ^2}\alpha  + co{s^2}\beta  + {\cos ^2}\gamma  = 1\)

HocTot.Nam.Name.Vn