Bài 21 trang 22 SGK Đại số và Giải tích 12 Nâng cao

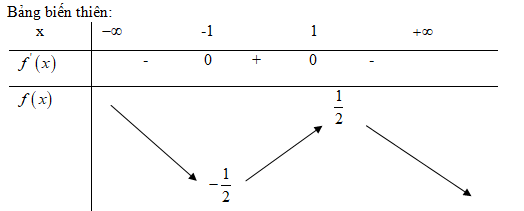
LG a

\(f\left( x \right) = {x \over {{x^2} + 1}};\)

Lời giải chi tiết:

TXĐ: \(D = {\mathbb{R}}\)

\(f'\left( x \right) = {{{x^2} + 1 - 2{x^2}} \over {{{\left( {{x^2} + 1} \right)}^2}}} = {{1 - {x^2}} \over {{{\left( {{x^2} + 1} \right)}^2}}}\)

\(f'\left( x \right) = 0 \Leftrightarrow \left[ \matrix{
x = 1,f\left( 1 \right) = {1 \over 2} \hfill \cr 
x = - 1,f\left( { - 1} \right) = - {1 \over 2} \hfill \cr} \right.\)

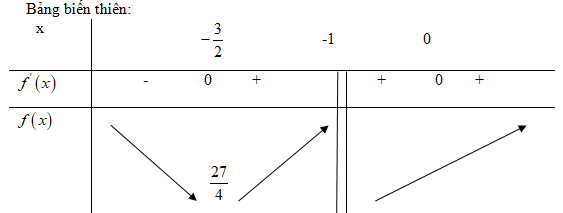
Hàm số đạt cực tiểu tại điểm \(x=-1\), giá trị cực tiểu \(f\left( { - 1} \right) =  - {1 \over 2}\).

Hàm số đạt cực đại tại điểm \(x=1\), giá trị cực đại \(f\left( 1 \right) = {1 \over 2}\).

LG b

\(f\left( x \right) = {{{x^3}} \over {x + 1}};\)

Lời giải chi tiết:

TXĐ: \(D = {\mathbb {R}}\backslash \left\{ { - 1} \right\}\)

\(\eqalign{
& f'\left( x \right) = {{3{x^2}\left( {x + 1} \right) - {x^3}} \over {{{\left( {x + 1} \right)}^2}}}\cr&= {{2{x^3} + 3{x^2}} \over {{{\left( {x + 1} \right)}^2}}} = \frac{{{x^2}\left( {2x + 3} \right)}}{{{{\left( {x + 1} \right)}^2}}}   \cr 
& f'\left( x \right) = 0 \Leftrightarrow {x^2}\left( {2x + 3} \right) = 0 \cr&\Leftrightarrow \left[ \matrix{
x = 0 \hfill \cr 
x = - {3 \over 2} \hfill \cr} \right. \cr 
& f\left( { - {3 \over 2}} \right) = {{27} \over 4} \cr} \)

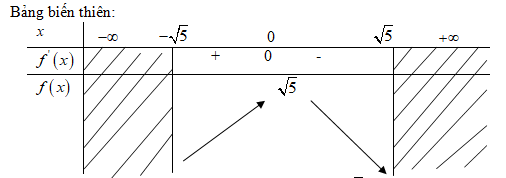
Hàm số đạt cực tiểu tại điểm \(x =  - {3 \over 2}\), giá trị cực tiểu \(f\left( { - {3 \over 2}} \right) = {{27} \over 4}\).

Hàm số không có cực đại.

LG c

\(f\left( x \right) = \sqrt {5 - {x^2}} ;\)

Lời giải chi tiết:

TXĐ: \(D = \left[ { - \sqrt 5 ;\sqrt 5 } \right]\)

\(f'\left( x \right) = {{ - 2x} \over {2\sqrt {5 - {x^2}} }} = {{ - x} \over {\sqrt {5 - {x^2}} }}\)

\(f'\left( x \right) = 0 \Leftrightarrow x = 0;f\left( 0 \right) = \sqrt 5 \)

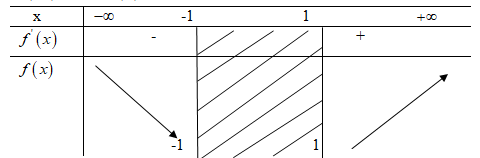
Hàm số đạt cực đại tại \(x=0\), giá trị cực đại \(f\left( 0 \right) = \sqrt 5 \).

Hàm số không có cực tiểu.

LG d

\(f\left( x \right) = x + \sqrt {{x^2} - 1} \).

Lời giải chi tiết:

\(f\left( x \right)\) xác định khi và chỉ khi \({x^2} - 1 \ge 0\) \( \Leftrightarrow x \le  - 1\) hoặc \(x \ge 1\).

TXĐ: \(D = \left( { - \infty ; - 1} \right] \cup \left[ {1; + \infty } \right)\)

\(f'\left( x \right) = 1 + {x \over {\sqrt {{x^2} - 1} }} = {{\sqrt {{x^2} - 1}  + x} \over {\sqrt {{x^2} - 1} }}\) 

\(f'\left( x \right) = 0 \Leftrightarrow \sqrt {{x^2} - 1} = - x\) \( \Leftrightarrow \left\{ \matrix{
x \le 0 \hfill \cr 
{x^2} - 1 = {x^2} \hfill \cr} \right.\) vô nghiệm

Hàm số nghịch biến trên \(\left( { - \infty ; - 1} \right]\) và đồng biến trên \(\left[ {1; + \infty } \right)\).

Hàm số không có cực trị.

Chú ý:

Để xét dấu nhanh và chính xác trong các khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( {1; + \infty } \right)\) thì ta chỉ cần cho x nhận 1 giá cụ thể thuộc khoảng đó. Chẳng hạn,

\(f'\left( { - 2} \right) < 0 \Rightarrow f'\left( x \right) < 0\) với mọi \(x <  - 1\).

\(f'\left( { - 2} \right) > 0 \Rightarrow f'\left( x \right) > 2\) với mọi \(x > 1\).

HocTot.Nam.Name.Vn