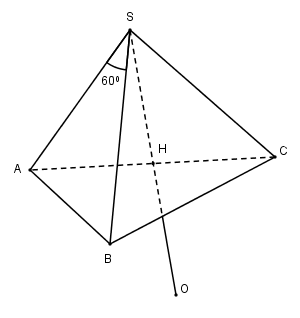
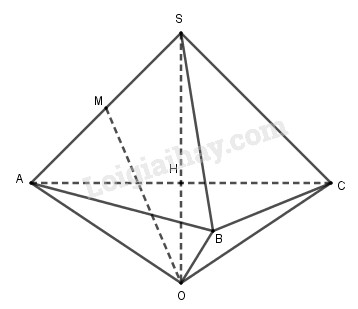
Bài 2 trang 63 SGK Hình học 12 Nâng cao

Đề bài

Xác định tâm và bán kính của mặt cầu ngoại tiếp hình chóp \(S.ABC\), biết \(SA = SB = SC = a\), \(\widehat {ASB} = {60^0},\widehat {BSC} = {90^0},\widehat {CSA} = {120^0}\)

Lời giải chi tiết

Áp dụng định lí Cosin trong tam giác \(SAB, SAC\) ta có:

\(\eqalign{
& A{B^2} = S{A^2} + S{B^2} - 2SA.SB.\cos {60^0} \cr 
& = {a^2} + {a^2} - 2{a^2}.{1 \over 2} = {a^2} \Rightarrow AB = a \cr 
& A{C^2} = S{A^2} + S{C^2} - 2SA.SC.\cos {120^0} \cr 
& = {a^2} + {a^2} - 2{a^2}\left( { - {1 \over 2}} \right) = 3{a^2}\cr & \Rightarrow AC = a\sqrt 3 \cr} \)

Trong tam giác vuông \(SBC\) có: \(B{C^2} = S{B^2} + S{C^2} = 2{a^2} \) \(\Rightarrow BC = a\sqrt 2 \)

Ta có: \(A{C^2} = A{B^2} + B{C^2} \Rightarrow \Delta ABC\) vuông tại \(B\).

Gọi \(H\) là trung điểm của \(AC\) thì \(H\) là tâm đường tròn ngoại tiếp tam giác ABC.

Vì \(SA = SB = SC\) nên \(SH \bot mp\left( {ABC} \right)\)

Và \(S{H^2} = S{C^2} - H{C^2} \) \(= {a^2} - {\left( {{{a\sqrt 3 } \over 2}} \right)^2}\) \( = {{{a^2}} \over 4} \Rightarrow SH = {a \over 2}\)

Gọi O là điểm đối xứng của S qua H.

Khi đó \(OS = 2SH = 2.\frac{a}{2} = a\).

Tam giác OAH vuông tại \(H\) nên theo Pitago ta có

\(OA = \sqrt {A{H^2} + O{H^2}} \) \( = \sqrt {{{\left( {\frac{{a\sqrt 3 }}{2}} \right)}^2} + {{\left( {\frac{a}{2}} \right)}^2}}  = a\)

Lại có SH là trục đường tròn ngoại tiếp tam giác ABC và \(O \in SH\) nên \(OA = OB = OC = a\).

Vậy \(OS = OA = OB = OC = a\) hay \(O\) là tâm mặt cầu ngoại tiếp hình chóp \(S.ABC\) và bán kính \(R = a\).

Cách khác:

Ta có: \(HA = HB = HC\), \(SA = SB = SC\) nên \(SH\) là trục đường tròn ngoại tiếp tam giác ABC

\( \Rightarrow \) tâm mặt cầu ngoại tiếp hình chóp S.ABC nằm trên \(SH\).

Gọi M là trung điểm của SA.

Trong \(\left( {SAC} \right)\), kẻ đường thẳng \(d\) đi qua M và vuông góc \(SA\) cắt \(SH\) tại \(O\)

(\(d\) là đường trung trực của \(SA\) )

Khi đó:

\(O \in SH \Rightarrow OA = OB = OC\)

\(O \in d \Rightarrow OS = OA\)

\( \Rightarrow \) \(OS = OA = OB = OC\)  hay O là tâm mặt cầu ngoại tiếp hình chóp S.ABC.

Xét \(\Delta SMO\) và \(\Delta SHA\) có:

\(\widehat S\) chung

\(\widehat {SMO} = \widehat {SHA} = {90^0}\)

\(\begin{array}{l} \Rightarrow \Delta SMO \sim \Delta SHA\left( {g - g} \right)\\ \Rightarrow \frac{{SM}}{{SH}} = \frac{{SO}}{{SA}} \Rightarrow SM.SA = SH.SO\\ \Rightarrow \frac{1}{2}SA.SA = SH.SO\\ \Rightarrow \frac{1}{2}{a^2} = \frac{a}{2}.SO \Rightarrow SO = a\end{array}\)

Vậy bán kính \(R = a\).

HocTot.Nam.Name.Vn